题目内容
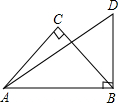 如图,∠ABD=∠C=90°,AC=BC,∠DAB=30°,AD=6,求BC的长.
如图,∠ABD=∠C=90°,AC=BC,∠DAB=30°,AD=6,求BC的长.
分析:在直角△ABD中,已知一边及锐角,就可以求出AB,则△ABC就满足解直角三角形的条件,因而就可以求出BC的长.
解答:解:在直角△ABD中cos∠DAB=
=cos30°=
∴AB=
×6=3
.
在直角△ABC中sin∠CAB=
=sin45°=
∴BC=
AB=
.
| AB |
| AD |
| ||
| 2 |
∴AB=
| ||
| 2 |
| 3 |
在直角△ABC中sin∠CAB=
| BC |
| AB |
| ||
| 2 |
∴BC=
| ||
| 2 |
3
| ||
| 2 |
点评:本题主要考查了解直角三角形的条件,已知三角形的一边与一个锐角,就可以求出另一个锐角与三角形的另外两边.

练习册系列答案
相关题目
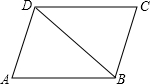 如图,△ABD≌△CDB,下面结论中不正确的是( )
如图,△ABD≌△CDB,下面结论中不正确的是( )| A、△ABD和△CDB的面积相等 | B、∠A+∠ABD=∠C+∠CBD | C、△ABD和△CDB的周长相等 | D、AD∥BC,且AD=BC |
 4、如图,∠ABD=90°,直线
4、如图,∠ABD=90°,直线 15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是
15、如图,∠ABD=∠CBD,DF∥AB,DE∥BC,则∠1与∠2的大小关系是 如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求
如图,△ABD中,点C、F分别为BD、AB上一点,AC、DF交于E,且CD=2BC,AE=2CE.求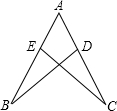 如图,△ABD≌△ACE,那么点B与点
如图,△ABD≌△ACE,那么点B与点