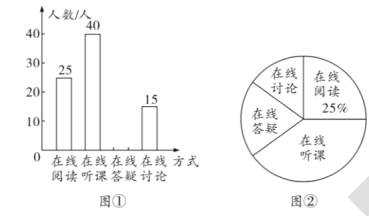
题目内容
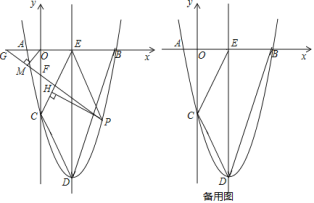
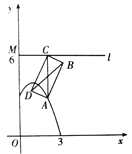
【题目】如图,点A在抛物线![]() 上,直线
上,直线![]() ⊥y轴于点M,AC⊥
⊥y轴于点M,AC⊥![]() 于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
于点C,以AC为对角线作矩形ABCD,若点M的坐标为(0,6),则BD的取值范围是_______.
【答案】![]()
【解析】
把二次函数的解析式化成顶点式和两点式,可得顶点坐标和与x轴的交点坐标,即可得出当A与顶点重合时,AC最短,当A在![]() 轴上时,AC最长,可求出AC的取值范围,根据矩形的性质可得AC=BD,即可得答案.
轴上时,AC最长,可求出AC的取值范围,根据矩形的性质可得AC=BD,即可得答案.
∵![]() =-(x+1)(x-3),
=-(x+1)(x-3),
∴顶点坐标为(1,4),与x轴的交点坐标为(-1,0)(3,0),
∵0≤x≤3,
∴当A与顶点重合时,AC最短,
当x=1时,y=-1+2+3=4,
∴AC=6-4=2;
当A在![]() 轴上时,AC最长,此时AC=6,
轴上时,AC最长,此时AC=6,
∴2≤AC≤6,
∵四边形ABCD是矩形,
∴AC=BD,
∴BD的取值范围是![]() .
.
故答案为:![]()

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目