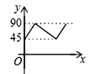
МвДҝДЪИЭ
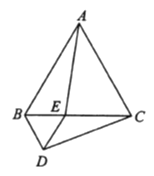
ЎҫМвДҝЎҝИзНјЈ¬ФЪ![]() ЦРЈ¬
ЦРЈ¬ ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cmЈ¬Иф¶Ҝөг
=3 cmЈ¬Иф¶Ҝөг![]() ҙУөг
ҙУөг![]() ҝӘКјЈ¬°ҙ
ҝӘКјЈ¬°ҙ![]() өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл1 cmЈ¬Йиіц·ўөДКұјдОӘ
өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл1 cmЈ¬Йиіц·ўөДКұјдОӘ![]() s.
s.
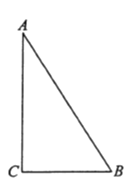
(1)Зуіц·ў2sәуЈ¬ ![]() өДГж»э.
өДГж»э.
(2) ![]() ОӘәОЦөКұЈ¬
ОӘәОЦөКұЈ¬ ![]() ОӘөИСьИэҪЗРО?
ОӘөИСьИэҪЗРО?
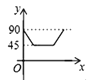
(3)БнУРТ»өг![]() Ј¬ҙУөг
Ј¬ҙУөг![]() ҝӘКјЈ¬°ҙ
ҝӘКјЈ¬°ҙ![]() өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл2 cmЈ¬Иф
өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл2 cmЈ¬Иф![]() БҪөгН¬Кұіц·ўЈ¬өұ
БҪөгН¬Кұіц·ўЈ¬өұ![]() ЦРУРТ»өгөҪҙпЦХөгКұЈ¬БнТ»өгТІНЈЦ№ФЛ¶Ҝ.өұ
ЦРУРТ»өгөҪҙпЦХөгКұЈ¬БнТ»өгТІНЈЦ№ФЛ¶Ҝ.өұ![]() ОӘәОЦөКұЈ¬ЦұПЯ
ОӘәОЦөКұЈ¬ЦұПЯ![]() °С
°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц?
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц?
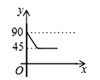
Ўҫҙр°ёЎҝ(1) ![]() өДГж»эОӘ
өДГж»эОӘ![]() cm2;(2) t=3s»т6s»т5.4s»т6.5sЈ¬
cm2;(2) t=3s»т6s»т5.4s»т6.5sЈ¬ ![]() ОӘөИСьИэҪЗРО;(3)өұ
ОӘөИСьИэҪЗРО;(3)өұ![]() ОӘ
ОӘ![]() s»т
s»т![]() sКұЈ¬ЦұПЯ
sКұЈ¬ЦұПЯ![]() °С
°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц.
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©АыУГ№ҙ№Й¶ЁАнөГіцAC=4cmЈ¬Ҫш¶шұнКҫіцAPөДіӨЈ¬Ҫш¶шөГіцҙр°ёЈ»
ЈЁ2Ј©·ЦБҪЦЦЗйҝцЈәўЩИфPФЪұЯACЙПКұЈ¬BC=CP=6cmЈ¬ҙЛКұУГөДКұјдОӘ6sЈ»ўЪИфPФЪABұЯЙПКұЈ¬УРИэЦЦҝЙДЬЈәiИфК№BP=CB=6cmЈ¬ҙЛКұAP=4cmЈ¬PФЛ¶ҜөДВ·іМОӘ4+8=12cmЈ¬УГөДКұјдОӘ12КұЈ»iiЈ©ИфCP=BC=6cmЈ¬№эCЧчCDЎНABУЪөгDЈ¬ёщҫЭГж»э·ЁЗуөГёЯCD=4.8cmЈ¬ЗуіцBP=2PD=7.2cmЈ¬өГіцPФЛ¶ҜөДВ·іМОӘ18-7.2=10.8cmЈ¬јҙҝЙөГіцҪб№ыЈ»ўЈЈ©ИфBP=CPЈ¬ФтЎПPCB=ЎПBЈ¬ЦӨіцPA=PCөГіцPA=PB=5cmЈ¬өГіцPөДВ·іМОӘ13cmЈ¬јҙҝЙөГіцҪб№ыЈ»
ЈЁ3Ј©·ЦБҪЦЦЗйҝцЈәўЩөұPЎўQГ»ПаУцЗ°ЈәPөгЧЯ№эөДВ·іМОӘtЈ¬QЧЯ№эөДВ·іМОӘ2tЈ¬ёщҫЭМвТвөГіц·ҪіМЈ¬Ҫв·ҪіМјҙҝЙЈ»ўЪөұPЎўQГ»ПаУцәуЈәөұPөгФЪABЙПЈ¬QФЪACЙПЈ¬ФтAP=t-8Ј¬AQ=2t-16Ј¬ёщҫЭМвТвөГіц·ҪіМЈ¬Ҫв·ҪіМјҙҝЙЈ»јҙҝЙөГіцҪб№ыЈ®
(1)ИзНјўЩЈ¬ТтОӘ![]() ,
, ![]() =5 cm,
=5 cm, ![]() =3 cm
=3 cm
ЛщТФ![]() cm
cm
¶Ҝөг![]() ҙУөг
ҙУөг![]() ҝӘКјЈ¬°ҙ
ҝӘКјЈ¬°ҙ![]() өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл1 cmЈ¬ЛщТФіц·ў2sәуЈ¬
өДВ·ҫ¶ФЛ¶ҜЈ¬ЗТЛЩ¶ИОӘГҝГл1 cmЈ¬ЛщТФіц·ў2sәуЈ¬ ![]() .
.
ТтОӘ![]()
ЛщТФ![]() өДГж»эОӘ
өДГж»эОӘ![]() cm2.
cm2.
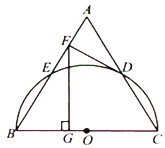
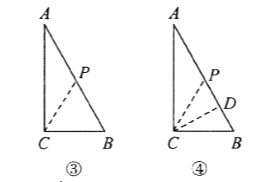
(2)ўЩИзНјўЪЈ¬өұөг![]() ФЪұЯ
ФЪұЯ![]() ЙПКұЈ¬
ЙПКұЈ¬ ![]() cmЈ¬ҙЛКұ
cmЈ¬ҙЛКұ![]() Ј¬
Ј¬ ![]() ОӘөИСьИэҪЗРО;
ОӘөИСьИэҪЗРО;
ўЪөұөг![]() ФЪ
ФЪ![]() ұЯЙПКұЈ¬УРИэЦЦЗйҝц:
ұЯЙПКұЈ¬УРИэЦЦЗйҝц:
ўс)ИзНјўЫЈ¬Иф![]() cmЈ¬ҙЛКұ
cmЈ¬ҙЛКұ![]() cmЈ¬өг
cmЈ¬өг![]() ФЛ¶ҜөДВ·іМОӘ
ФЛ¶ҜөДВ·іМОӘ![]() (cm)Ј¬ҙЛКұ
(cm)Ј¬ҙЛКұ![]() Ј¬
Ј¬ ![]() ОӘөИСьИэҪЗРО;
ОӘөИСьИэҪЗРО;
ўт)ИзНјўЬЈ¬Иф![]() cmЈ¬№эөг
cmЈ¬№эөг![]() ЧчРұұЯ
ЧчРұұЯ![]() өДёЯҪ»
өДёЯҪ»![]() УЪөг
УЪөг![]() Ј¬ёщҫЭГж»э·ЁЗуөГёЯОӘ
Ј¬ёщҫЭГж»э·ЁЗуөГёЯОӘ![]() cmЈ¬ЛщТФ
cmЈ¬ЛщТФ![]() cmЈ¬ЛщТФ
cmЈ¬ЛщТФ![]() cmЈ¬ЛщТФөг
cmЈ¬ЛщТФөг![]() ФЛ¶ҜөДВ·іМОӘ
ФЛ¶ҜөДВ·іМОӘ![]() (cm)Ј¬ҙЛКұ
(cm)Ј¬ҙЛКұ![]() Ј¬
Ј¬ ![]() ОӘөИСьИэҪЗРО
ОӘөИСьИэҪЗРО
ўу)ИзНјўЭЈ¬Иф![]() Ј¬ҙЛКұ
Ј¬ҙЛКұ![]() УҰёГОӘРұұЯ
УҰёГОӘРұұЯ![]() өДЦРөгЈ¬өг
өДЦРөгЈ¬өг![]() ФЛ¶ҜөДВ·іМОӘ
ФЛ¶ҜөДВ·іМОӘ![]() (cm)Ј¬ҙЛКұЛщУГөДКұјдОӘ
(cm)Ј¬ҙЛКұЛщУГөДКұјдОӘ![]() sЈ¬
sЈ¬ ![]() ОӘөИСьИэҪЗРО.
ОӘөИСьИэҪЗРО.
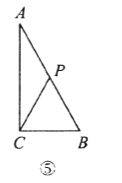
(3)ИзНјўЮЈ¬өұөг![]() ФЪ
ФЪ![]() ЙПЈ¬өг
ЙПЈ¬өг![]() ФЪ
ФЪ![]() ЙПКұЈ¬Фт
ЙПКұЈ¬Фт![]() Ј¬
Ј¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() s;
s;
ИзНјўЯЈ¬өұөг![]() ФЪ
ФЪ![]() ЙПЈ¬өг
ЙПЈ¬өг![]() ФЪ
ФЪ![]() ЙПКұЈ¬Фт
ЙПКұЈ¬Фт![]() Ј¬
Ј¬ ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() sЈ¬ЛщТФөұ
sЈ¬ЛщТФөұ![]() ОӘ
ОӘ![]() »т
»т![]() КұЈ¬ЦұПЯ
КұЈ¬ЦұПЯ![]() °С
°С![]() өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц.
өДЦЬіӨ·ЦіЙПаөИөДБҪІҝ·Ц.



 Т»ПЯГыКҰИЁНюЧчТөұҫПөБРҙр°ё
Т»ПЯГыКҰИЁНюЧчТөұҫПөБРҙр°ё