题目内容
 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC= ,则
,则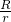 的值为
的值为
- A.

- B.

- C.2
- D.3
C
分析:根据切线长定理先证明∠ACB=90°,得直角三角形ABC;再由tan∠ABC= =
= ,得两圆弦长的比;进一步求半径的比.
,得两圆弦长的比;进一步求半径的比.
解答:如图,连接O2B,O1A,过点C作两圆的公切线CF,交于AB于点F,作O1E⊥AC,O2D⊥BC,
由垂径定理可证得点E,点D分别是AC,BC的中点,
由弦切角定理知,
∠ABC=∠FCB= ∠BO2C,∠BAC=∠FCA=
∠BO2C,∠BAC=∠FCA= ∠AO1C,
∠AO1C,
∵AO1∥O2B,
∴∠AO1C+∠BO2C=180°,
∴∠FCB+∠FCA=∠ACB=90°,
即△ACB是直角三角形,
∴∠ABC=∠BO2D=∠ACO1,
设∠ABC=∠BO2D=∠ACO1=β,
则有sinβ= ,cosβ=
,cosβ= ,
,
∴tanβ=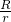 •
• =
=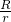 •
• ,
,
∴(tanβ)2=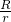 =2.
=2.
故选C.
点评:本题综合性较强,综合了圆的有关知识,所以学生所学的知识要系统起来,不可单一.
分析:根据切线长定理先证明∠ACB=90°,得直角三角形ABC;再由tan∠ABC=
 =
= ,得两圆弦长的比;进一步求半径的比.
,得两圆弦长的比;进一步求半径的比.解答:如图,连接O2B,O1A,过点C作两圆的公切线CF,交于AB于点F,作O1E⊥AC,O2D⊥BC,

由垂径定理可证得点E,点D分别是AC,BC的中点,
由弦切角定理知,
∠ABC=∠FCB=
 ∠BO2C,∠BAC=∠FCA=
∠BO2C,∠BAC=∠FCA= ∠AO1C,
∠AO1C,∵AO1∥O2B,
∴∠AO1C+∠BO2C=180°,
∴∠FCB+∠FCA=∠ACB=90°,
即△ACB是直角三角形,
∴∠ABC=∠BO2D=∠ACO1,
设∠ABC=∠BO2D=∠ACO1=β,
则有sinβ=
 ,cosβ=
,cosβ= ,
,∴tanβ=
 •
• =
= •
• ,
,∴(tanβ)2=
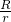 =2.
=2.故选C.
点评:本题综合性较强,综合了圆的有关知识,所以学生所学的知识要系统起来,不可单一.

练习册系列答案
相关题目
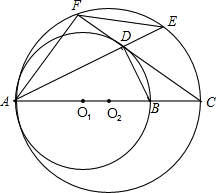 O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.
O1于点D,AD的延长线交⊙O2于点E,连接AF、EF、BD.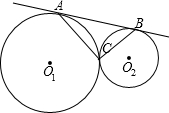 已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=
已知:如图,⊙O1与⊙O2外切于C点,AB一条外公切线,A、B分别为切点,连接AC、BC.设⊙O1的半径为R,⊙O2的半径为r,若tan∠ABC=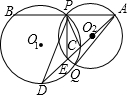 (1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且
(1998•南京)已知,如图,⊙O1与⊙O2相交,点P是其中一个交点,点A在⊙O2上,AP的延长线交⊙O1于点B,AO2的延长线交⊙O1于点C、D,交⊙O2于点E,连接PC、PE、PD,且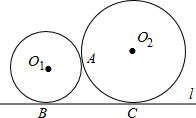 已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.
已知:如图,⊙O1与⊙O2外切于A点,直线l与⊙O1、⊙O2分别切于B,C点,若⊙O1的半径r1=2cm,⊙O2的半径r2=3cm.求BC的长.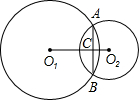 已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=
已知:如图,⊙O1与⊙O2相交于A、B,若两圆半径分别为12和5,O1O2=13,则AB=