Question

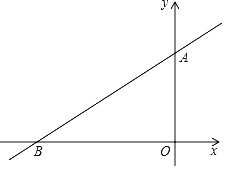
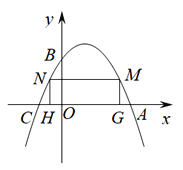
【题目】如图，将一块含的三角板（）放置在坐标系中，直角顶点与原点重合，另两个顶点、分别在反比例函数和的图像上，的值为___________.

Answer 1

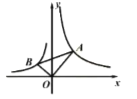
【答案】

【解析】

作AE⊥x轴，BF⊥x轴，根据相似三角形面积比等于相似比的平方得出，再根据直角三角形30°所对的直角边等于斜边一半及勾股定理确定AO与BO的比值，从而求出△BOF的面积，再根据反比例函数k值的几何意义求出k值.

解：如图，作AE⊥x轴，BF⊥x轴，垂足为E，F，

∵A点在反比例函数上，

∴S△AOE=，

∵∠AOB=∠AEO=∠BFO=90° ，

∴∠AOE=∠OBF=90°-∠BOF

∴△AOE∽△OBF，

∴

在Rt△AOB中，∠BAO=30°,

∴ ,

∴

∴S△BOF=×2=

∴ ，

∴.

故答案为：