题目内容
23、已知：如图，在直角坐标系中，点A，B分别是x轴，y轴上的任意两点，BE是∠ABy的平分线，BE的方向延长线与∠OAB的角平分线交于点C，则∠ACB=45°
．分析：先确定∠ABy与∠OAB的关系，∠ABy=∠OAB+90°，再根据角平分线和三角形的外角求得∠ACB的度数．
解答：解：∵∠ABy+∠ABO=180°，∠OAB+90°+∠ABO=180°，
∴∠ABy=∠OAB+90°，
∵BE是∠ABy的平分线，AC平分∠OAB，
∴∠ABy=2∠ABE，∠OAB=2∠BAC，
∵∠ABE=∠ACB+∠BAC，∴2∠ABE=2∠BAC+90°，
即2∠ACB+2∠BAC=2∠BAC+90°，∴∠ACB=45°．
∴∠ABy=∠OAB+90°，
∵BE是∠ABy的平分线，AC平分∠OAB，
∴∠ABy=2∠ABE，∠OAB=2∠BAC，
∵∠ABE=∠ACB+∠BAC，∴2∠ABE=2∠BAC+90°，
即2∠ACB+2∠BAC=2∠BAC+90°，∴∠ACB=45°．
点评：本题考查了角平分线的性质以及三角形的一个外角等于和它不相邻的两个内角的和．
练习册系列答案
相关题目
的图象的一个分支位于第一象限．
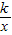的图象的图象上，求k的值；
S1？
的图象与y轴交于点A，
的图象分别交于点M，N，已知△AOB的面积为1，点M的纵坐
时x的取值范围。
中，四边形OABC是矩形，点A，C的坐
＝－
＋
交折线O－A－B于点E．
