题目内容
计算:
(1)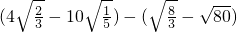 ;
;
(2)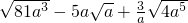 ;
;
(3)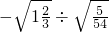 ;
;
(4)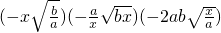 ;
;
(5)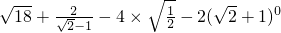 ;
;
(6)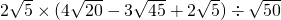 .
.
解:(1)原式=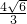 -2
-2 -
- +4
+4 =
= +2
+2 ;
;
(2)原式=9a -5a
-5a +6a
+6a =10a
=10a ;
;
(3)原式=-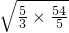 =-
=- =-3
=-3 ;
;
(4)原式=-x•(- )•(-2ab)•
)•(-2ab)•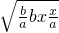 =-2a2b•
=-2a2b•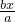 =-2ab2x;
=-2ab2x;
(5)原式=3 +2
+2 +2-2
+2-2 -2=3
-2=3 ;
;
(6)原式=2 ×(8
×(8 -9
-9 +2
+2 )÷5
)÷5 =2
=2 ×
× ÷5
÷5 =
= .
.
分析:(1)先把各二次根式化为最简二次根式得到原式=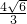 -2
-2 -
- +4
+4 ,然后合并同类二次根式;
,然后合并同类二次根式;
(2)先把各二次根式化为最简二次根式原式=9a -5a
-5a +6a
+6a ,然后合并同类二次根式;
,然后合并同类二次根式;
(3)利用二次根式的除法法则进行计算;
(4)利用二次根式的乘法法则进行计算;
(5)根据零指数幂的意义和分母有理化得到原式=3 +2
+2 +2-2
+2-2 -2,然后合并同类二次根式;
-2,然后合并同类二次根式;
(6)先把各二次根式化为最简二次根式得到原式=2 ×(8
×(8 -9
-9 +2
+2 )÷5
)÷5 ,再把括号内合并,然后进行二次根式的乘除运算.
,再把括号内合并,然后进行二次根式的乘除运算.
点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.
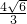 -2
-2 -
- +4
+4 =
= +2
+2 ;
;(2)原式=9a
 -5a
-5a +6a
+6a =10a
=10a ;
;(3)原式=-
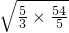 =-
=- =-3
=-3 ;
;(4)原式=-x•(-
 )•(-2ab)•
)•(-2ab)•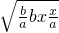 =-2a2b•
=-2a2b•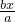 =-2ab2x;
=-2ab2x;(5)原式=3
 +2
+2 +2-2
+2-2 -2=3
-2=3 ;
;(6)原式=2
 ×(8
×(8 -9
-9 +2
+2 )÷5
)÷5 =2
=2 ×
× ÷5
÷5 =
= .
.分析:(1)先把各二次根式化为最简二次根式得到原式=
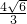 -2
-2 -
- +4
+4 ,然后合并同类二次根式;
,然后合并同类二次根式;(2)先把各二次根式化为最简二次根式原式=9a
 -5a
-5a +6a
+6a ,然后合并同类二次根式;
,然后合并同类二次根式;(3)利用二次根式的除法法则进行计算;
(4)利用二次根式的乘法法则进行计算;
(5)根据零指数幂的意义和分母有理化得到原式=3
 +2
+2 +2-2
+2-2 -2,然后合并同类二次根式;
-2,然后合并同类二次根式;(6)先把各二次根式化为最简二次根式得到原式=2
 ×(8
×(8 -9
-9 +2
+2 )÷5
)÷5 ,再把括号内合并,然后进行二次根式的乘除运算.
,再把括号内合并,然后进行二次根式的乘除运算.点评:本题考查了二次根式的混合运算:先把各二次根式化为最简二次根式,在进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂.

练习册系列答案
相关题目
