题目内容
如图1,平面之间坐标系中,等腰直角三角形的直角边BC在x轴正半轴上滑动,点C的坐标为(t,0),直角边AC=4,经过O,C两点做抛物线 (a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)
(a为常数,a>0),该抛物线与斜边AB交于点E,直线OA:y2=kx(k为常数,k>0)

(1)填空:用含t的代数式表示点A的坐标及k的值:A ,k= ;
(2)随着三角板的滑动,当a= 时:
时:
①请你验证:抛物线 的顶点在函数
的顶点在函数 的图象上;
的图象上;
②当三角板滑至点E为AB的中点时,求t的值;
(3)直线OA与抛物线的另一个交点为点D,当t≤x≤t+4,|y2﹣y1|的值随x的增大而减小,当x≥t+4时,|y2﹣y1|的值随x的增大而增大,求a与t的关系式及t的取值范围.
解:(1)∵点C的坐标为(t,0),直角边AC=4,∴点A的坐标是(t,4)。
∵直线OA:y2=kx(k为常数,k>0),∴4=kt,则 (k>0)。
(k>0)。
(2)①当a= 时,
时, ,其顶点坐标为
,其顶点坐标为 。
。
对于 ,当x=
,当x= 时,
时,
∴点 在抛物线
在抛物线 上。
上。
∴当a= 时,抛物线
时,抛物线 的顶点在函数
的顶点在函数 的图象上。
的图象上。
②如图1,过点E作EK⊥x轴于点K,

∵AC⊥x轴,∴AC∥EK。
∵点E是线段AB的中点,∴K为BC的中点。
∴EK是△ACB的中位线。
∴EK= AC=2,CK=
AC=2,CK= BC=2。∴E(t+2,2)。
BC=2。∴E(t+2,2)。
∵点E在抛物线 上,
上,
∴ ,解得t=2。
,解得t=2。
∴当三角板滑至点E为AB的中点时,t=2。
(3)如图2,由 得
得 ,
,

解得 ,或x=0(不合题意,舍去)。
,或x=0(不合题意,舍去)。
∴点D的横坐标是 。
。
当 时,|y2﹣y1|=0,由题意得
时,|y2﹣y1|=0,由题意得 ,即
,即 。
。
又 ,
,
∴当 时,
时, 取得最大值。
取得最大值。
又当 时,
时, 取得最小值0,
取得最小值0,
∴当 时,
时, 的值随x的增大而减小,当
的值随x的增大而减小,当 时,
时, 的值随x的增大而增大。
的值随x的增大而增大。
由题意,得 ,将
,将 代入得
代入得 ,解得
,解得 。
。
综上所述,a与t的关系式为 ,t的取值范围为
,t的取值范围为 。
。
【解析】
试题分析:(1)根据题意易得点A的横坐标与点C的相同,点A的纵坐标即是线段AC的长度;把点A的坐标代入直线OA的解析式来求k的值:
(2)①求得抛物线y1的顶点坐标,然后把该坐标代入函数 ,若该点满足函数解析式
,若该点满足函数解析式 ,即表示该顶点在函数
,即表示该顶点在函数 图象上;反之,该顶点不在函数
图象上;反之,该顶点不在函数 图象上。
图象上。
②如图1,过点E作EK⊥x轴于点K.则EK是△ACB的中位线,所以根据三角形中位线定理易求点E的坐标,把点E的坐标代入抛物线 即可求得t=2。
即可求得t=2。
(3)如图2,根据抛物线与直线相交可以求得点D横坐标是 ,则
,则 ,由此可以求得a与t的关系式。由
,由此可以求得a与t的关系式。由 求得
求得 取得最大值时的x值
取得最大值时的x值 ,同时由
,同时由 时,
时, 取得最小值0,得出当
取得最小值0,得出当 时,
时, 的值随x的增大而减小,当
的值随x的增大而减小,当 时,
时, 的值随x的增大而增大。从而由题意,得
的值随x的增大而增大。从而由题意,得 ,结合
,结合 ,求出t的取值范围。
,求出t的取值范围。

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案

 时:
时: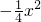 的图象上;
的图象上;

 时:
时: 的图象上;
的图象上;