Question

【题目】如图所示，直线交轴于点，交轴于点，且、满足.

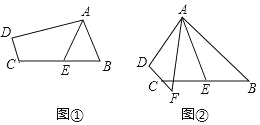
（1）如图1，请求出、的值以及的度数；

（2）如图1，若点为的中点，点为轴正半轴上一动点，连接，过作交轴于点，当点在轴正半轴上运动的过程中，的值是否发生改变？如发生改变，求出变化范围；若不改变，求该式子的值。

（3）如图2，若点为轴负半轴上一点，连接，过点作于点，交于点，请连接并求出的度数.

Answer 1

【答案】（1），，；（2）S△BDMS△ADN的值不发生改变，S△BDMS△AND=4；（3）∠OHP=45°.

【解析】

（1）由，求出a、b的值，然后得到OA=OB，则△OAB是等腰直角三角形，即可得到的度数；

（2）连接OD，易证△ODM≌△ADN，从而有S△ODM=S△ADN，由此可得 =S△BDM-S△ODM=S△BOD=S△AOB=4；

（3）根据题意，先证明△OAP≌△OBC（ASA），得到OP=OC，过O分别作OM⊥CB于M点，作ON⊥HA于N点，得到△COM≌△PON，得到OM=ON，则HO平分∠CHA，即可得到的度数.

解：（1）∵，

∴，，

∴，，

∴点A为（4，0），点B为（0，），

∴OA=OB=4，

∴△OAB是等腰直角三角形，

∴；

（2）S△BDMS△ADN的值不发生改变，等于4．

理由如下：连接OD，如图：

∵∠AOB=90°，OA=OB，D为AB的中点，

∴OD⊥AB，∠BOD=∠AOD=45°，OD=DA=BD

∴∠OAD=45°，∠MOD=90°+45°=135°，

∴∠DAN=135°=∠MOD．

∵MD⊥ND即∠MDN=90°，

∴∠MDO=∠NDA=90°∠MDA．

在△ODM与△ADN中，

，

∴△ODM≌△ADN（ASA），

∴S△ODM=S△AND

∴S△BDMS△AND

=S△BDMS△ODM

=S△BOD=S△AOB

=AOBO

=；

（3）如图：

∵AH⊥BC即∠AHC=90°，∠COB=90°

∴∠HAC+∠ACH=∠OBC+∠OCB=90°，

∴∠HAC=∠OBC．

在△OAP与△OBC中，

，

∴△OAP≌△OBC（ASA），

∴OP=OC=1，

过O分别作OM⊥CB于M点，作ON⊥HA于N点，如图：

在四边形OMHN中，∠MON=360°3×90°=90°，

∴∠COM=∠PON=90°∠MOP．

在△COM与△PON中，

，

∴△COM≌△PON（AAS），

∴OM=ON．

∵OM⊥CB，ON⊥HA，

∴HO平分∠CHA，

∴∠OHP=∠CHA=45°.