ЬтФПФкШн
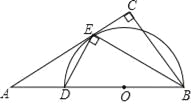
ЁОЬтФПЁПШчЭМЂйЃЌЫФБпаЮOACBЮЊГЄЗНаЮЃЌAЃЈЉ6ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЌжБЯпlЮЊКЏЪ§yЃНЉ2xЉ5ЕФЭМЯѓЃЎ
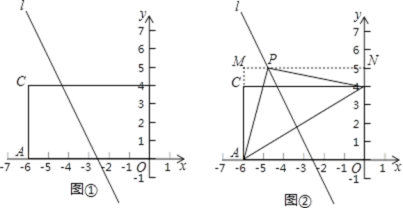
ЃЈ1ЃЉЕуCЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉШєЕуPдкжБЯпlЩЯЃЌЁїAPBЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯAPBЃН90ЁуЃЌЧѓЕуPЕФзјБъЃЛ
аЁУїЕФЫМПМЙ§ГЬШчЯТЃК
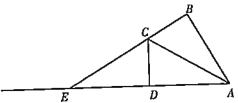
ЕквЛВНЃКЬэМгИЈжњЯпЃЌШчЭМЂкЃЌЙ§ЕуPзїMNЁЮxжсЃЌгыyжсНЛгкЕуNЃЌгыACЕФбгГЄЯпНЛгкЕуMЃЛ
ЕкЖўВНЃКжЄУїЁїMPAЁеЁїNBPЃЛ
ЕкШ§ВНЃКЩшNBЃНmЃЌСаГіЙигкmЕФЗНГЬЃЌНјЖјЧѓЕУЕуPЕФзјБъЃЎ
ЧыФуИљОнаЁУїЕФЫМПМЙ§ГЬЃЌаДГіЕкЖўВНКЭЕкШ§ВНЕФЭъећНтД№Й§ГЬЃЛ
ЃЈ3ЃЉШєЕуPдкжБЯпlЩЯЃЌЕуQдкЯпЖЮACЩЯЃЈВЛгыЕуAжиКЯЃЉЃЌЁїQPBЮЊЕШбќжБНЧШ§НЧаЮЃЌжБНгаДГіЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈЉ6ЃЌ4ЃЉЃЛЃЈ2ЃЉЃЈЉ5ЃЌ5ЃЉЃЌМћНтЮіЃЛЃЈ3ЃЉЃЈЉ3ЃЌ1ЃЉЛђЃЈЉ7ЃЌ9ЃЉ
ЁОНтЮіЁП
(1)ИљОнОиаЮЕФаджЪПЩвдЧѓЕУЃЎ
(2)гЩЁїMPAЁеЁїNBPСаГіЗНГЬМДПЩЧѓНтЃЎ
(3)ЗжШ§жжЧщаЮЬжТлЂй![]() ЃЌРћгУЭМ1жа
ЃЌРћгУЭМ1жа![]() МДПЩЧѓГіЃЎ
МДПЩЧѓГіЃЎ
Ђк![]() ЃЌРћгУЭМ2жа
ЃЌРћгУЭМ2жа![]() МДПЩЧѓГіЃЎ
МДПЩЧѓГіЃЎ
Ђл![]() ЃЌРћгУЭМ3жа
ЃЌРћгУЭМ3жа![]() МДПЩЧѓГіЃЎ
МДПЩЧѓГіЃЎ
НтЃКЃЈ1ЃЉЁпЫФБпаЮAOBCЪЧОиаЮЃЌ
![]() ЃЌ
ЃЌ
ЁрЕуCЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊC![]() ЃЎ
ЃЎ
ЃЈ2ЃЉИљОнЬтвтЕУЃК![]() ЃЌ
ЃЌ
Ёп![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуPЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЩшЕуQЕФзјБъЮЊ![]() ЃЌ
ЃЌ
Зж3жжЧщПіЬжТлЃК
ЂйЕБ![]() ЪБЃЌШчгвЭМЃЌЙ§ЕуPзї
ЪБЃЌШчгвЭМЃЌЙ§ЕуPзї![]() жсгкЕуMЃЌЕуQзї
жсгкЕуMЃЌЕуQзї![]() жсгкЕуNЃЌ
жсгкЕуNЃЌ

![]() ,
,
![]() ,
,
дк![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
ДњШы![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
ДЫЪБЕуQВЛдкЯпЖЮACЪБЃЌВЛКЯЬтвтЃЌЩсЦњЃЎ
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ
ШєЕуPдкBQЩЯЗНЃЌМДЮЊЃЈ2ЃЉЕФЧщПіЃЌДЫЪБЕуQгыЕуAжиКЯЃЌгЩгкЬтЩшжаЙцЖЈЕуQВЛгыЕуAжиКЯЃЌЙЪДЫжжЧщПіЩсШЅЃЛ
ШєЕуPдкBQЯТЗНЃЌШчгвЭМЃЌЙ§ЕуPзї![]() гкЕуNЃЌзї
гкЕуNЃЌзї![]() жсгкЕуMЃЌ
жсгкЕуMЃЌ

Щш![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ

![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
АбPзјБъДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌ
ЃЌ
НтЕУЃК![]() .
.
ДЫЪБЕуPЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЂлЕБ![]() ЪБШчгвЭМЃЌЙ§ЕуQзї
ЪБШчгвЭМЃЌЙ§ЕуQзї![]() жсгкЕуMЃЌЙ§ЕуPзї
жсгкЕуMЃЌЙ§ЕуPзї![]() ДЙзуЮЊNЃЌ
ДЙзуЮЊNЃЌ

Щш![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
дк![]() жаЃЌ
жаЃЌ
 ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
АбPзјБъДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌДЫЪБЕуPЕФзјБъЮЊ
ЃЌДЫЪБЕуPЕФзјБъЮЊ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ

 ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ
ХргХКУОэЕЅдЊМгЦкФЉОэЯЕСаД№АИ