题目内容
【题目】附加题
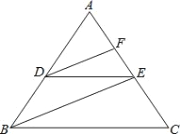
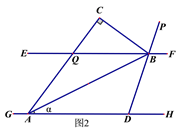
如图,直线EF∥GH,点B、A分别在直线EF、GH上,连接AB,在AB左侧作△ABC,其中∠ACB=90°,且∠DAB=∠BAC,直线BD平分∠FBC交直线GH于D.
(1)若点C恰在EF上,如图1,则∠DBA=______.
(2)将A点向左移动,其它条件不变,如图2,设∠BAD=α.
①试求∠EBC和∠PBC的大小(用α表示).
②问∠DBA的大小是否发生改变?若不变,求∠DBA的值;若变化,说明理由.
(3)若将题目条件“∠ACB=90°”,改为:“∠ACB=β”,其它条件不变,那么∠DBA= ______.(直接写出结果,不必证明)

【答案】 (1)45°;
(2)①∠EBC=90°﹣∠1﹣∠3=90°﹣2α,∠PBC=![]() (180°﹣∠EBC)=45°+α;
(180°﹣∠EBC)=45°+α;
②不变,∠DBA=45°; (3)∠DBA=![]() β.
β.
【解析】 试题分析:(1)根据两直线平行,同旁内角互补求出∠CAD=90°,然后求出∠BAC=45°,从而得到∠ABC=45°,再根据BD平分∠FBC求出∠DBC=90°,然后求解即可;
(2)①EF∥GH,得出∠2=∠3,进一步得出∠1=∠3,利用三角形的内角和得出∠EBC,利用平角的意义得出∠PBC;
②根据两直线平行,内错角相等可得∠2=∠3,再根据三角形的内角和定理表示出∠4,然后表示∠5,再利用平角等于180°列式表示出∠DBA整理即可得解.
(3)根据(2)的结论计算即可得解.
本题解析:

①∵EF∥GH,∴∠2=∠3,∵∠1=∠2= ![]() ,∴∠1=∠3=
,∴∠1=∠3= ![]() ,∵∠ACB=
,∵∠ACB=![]() ,
,
∴∠EBC=![]() ∠1∠3=
∠1∠3=![]() 2
2![]() ,∠PBC=
,∠PBC=![]() (
(![]() ∠EBC)=
∠EBC)= ![]() +
+ ![]() ;
;
②设∠DAB=∠BAC= ![]() ,即∠1=∠2=
,即∠1=∠2= ![]() ,∵EF∥GH,∴∠2=∠3,
,∵EF∥GH,∴∠2=∠3,
在△ABC内,∠4=![]() ∠ACB∠1∠3=
∠ACB∠1∠3=![]() ∠ACB2
∠ACB2![]() ,
,
∵直线BD平分∠FBC,∴∠5=![]() (
(![]() ∠4)=
∠4)= ![]() (
(![]()
![]() +∠ACB+2
+∠ACB+2![]() )=
)= ![]() ∠ACB+
∠ACB+ ![]() ,
,
∴∠DBA=![]() ∠3∠4∠5,=
∠3∠4∠5,= ![]()
![]() (
(![]() ∠ACB2
∠ACB2![]() )(
)( ![]() ∠ACB+
∠ACB+ ![]() ),=
),= ![]()
![]()
![]() +∠ACB+2
+∠ACB+2![]()
![]() ∠ACB
∠ACB ![]() x,=
x,= ![]() ∠ACB,=
∠ACB,= ![]() ×
×![]() ,=45;
,=45;
(3)由(2)可知,
设∠DAB=∠BAC= ![]() ,即∠1=∠2=
,即∠1=∠2= ![]() ,∵EF∥GH,∴∠2=∠3,
,∵EF∥GH,∴∠2=∠3,
在△ABC内,∠4=![]() ∠ACB∠1∠3=
∠ACB∠1∠3=![]() ∠ACB2
∠ACB2![]() ,∵直线BD平分∠FBC,
,∵直线BD平分∠FBC,
∴∠5=![]() (
(![]() ∠4)=
∠4)= ![]() (
(![]()
![]() +∠ACB+2
+∠ACB+2![]() )=12
)=12![]() ∠ACB+
∠ACB+ ![]() ,
,
∴∠DBA=![]() ∠3∠4∠5,=180
∠3∠4∠5,=180 ![]() (
(![]() ∠ACB2
∠ACB2![]() )(
)(![]() ∠ACB+
∠ACB+ ![]() ),=
),= ![]()
![]()
![]() +∠ACB+2
+∠ACB+2![]() 12
12![]() ∠ACB
∠ACB ![]() ,=
,=![]() ∠ACB,∠ACB=
∠ACB,∠ACB= ![]() 时,∠DBA=
时,∠DBA= ![]()

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案