题目内容
 四边形ABCD的对角线AC、BD的长分别为m、n.
四边形ABCD的对角线AC、BD的长分别为m、n.
(1)当AC⊥BD时(如图1),请证明,四边形ABCD的面积 ;
;
(2)当AC、BD所夹的锐角为θ时(如图2),猜想四边形ABCD的面积S与m、n、θ的关系,并证明.
(1)证明:如图1,AC与BD的垂足为O点,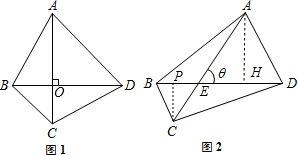
∵AC⊥BD,
∴S△ABD= AO•BD,S△CBD=
AO•BD,S△CBD= CO•BD,
CO•BD,
∴四边形ABCD的面积=S△ABD+S△CBD= AO•BD+
AO•BD+ CO•BD=
CO•BD= BD•(AO+CO)=
BD•(AO+CO)= BD•AC=
BD•AC= mn;
mn;
(2)解:作AH⊥BD于H点,CP⊥BD于P点,AC与BD交于E点,如图2,
在RtAEH中,sinθ=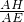 ,即AH=AE•sinθ,
,即AH=AE•sinθ,
在RtCPE中,sin∠PEC= ,PC=CE•sin∠PEC=CE•sinθ,
,PC=CE•sin∠PEC=CE•sinθ,
∵S△ABD= AH•BD,S△CBD=
AH•BD,S△CBD= CP•BD,
CP•BD,
∴四边形ABCD的面积S=S△ABD+S△CBD= AH•BD+
AH•BD+ CP•BD=
CP•BD= AE•sinθ•BD+
AE•sinθ•BD+ CE•sinθ•BD=
CE•sinθ•BD= BD•(AE+CE)•sinθ=
BD•(AE+CE)•sinθ= BD•AC•sinθ=
BD•AC•sinθ= m•n•sinθ.
m•n•sinθ.
分析:(1)根据三角形面积公式得到S△ABD= AO•BD,S△CBD=
AO•BD,S△CBD= CO•BD,然后把两个三角形面积相加即可得到结论;
CO•BD,然后把两个三角形面积相加即可得到结论;
(2)作AH⊥BD于H点,CP⊥BD于P点,AC与BD交于E点,根据正弦的定义得到AH=AE•sinθ,PC=CE•sin∠PEC=CE•sinθ,然后再根据三角形面积公式得到S△ABD= AH•BD,S△CBD=
AH•BD,S△CBD= CP•BD,再把两个三角形面积相加即可得到四边形ABCD的面积S=
CP•BD,再把两个三角形面积相加即可得到四边形ABCD的面积S= m•n•sinθ.
m•n•sinθ.
点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了三角形面积公式.

∵AC⊥BD,
∴S△ABD=
 AO•BD,S△CBD=
AO•BD,S△CBD= CO•BD,
CO•BD,∴四边形ABCD的面积=S△ABD+S△CBD=
 AO•BD+
AO•BD+ CO•BD=
CO•BD= BD•(AO+CO)=
BD•(AO+CO)= BD•AC=
BD•AC= mn;
mn;(2)解:作AH⊥BD于H点,CP⊥BD于P点,AC与BD交于E点,如图2,
在RtAEH中,sinθ=
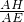 ,即AH=AE•sinθ,
,即AH=AE•sinθ,在RtCPE中,sin∠PEC=
 ,PC=CE•sin∠PEC=CE•sinθ,
,PC=CE•sin∠PEC=CE•sinθ,∵S△ABD=
 AH•BD,S△CBD=
AH•BD,S△CBD= CP•BD,
CP•BD,∴四边形ABCD的面积S=S△ABD+S△CBD=
 AH•BD+
AH•BD+ CP•BD=
CP•BD= AE•sinθ•BD+
AE•sinθ•BD+ CE•sinθ•BD=
CE•sinθ•BD= BD•(AE+CE)•sinθ=
BD•(AE+CE)•sinθ= BD•AC•sinθ=
BD•AC•sinθ= m•n•sinθ.
m•n•sinθ.分析:(1)根据三角形面积公式得到S△ABD=
 AO•BD,S△CBD=
AO•BD,S△CBD= CO•BD,然后把两个三角形面积相加即可得到结论;
CO•BD,然后把两个三角形面积相加即可得到结论;(2)作AH⊥BD于H点,CP⊥BD于P点,AC与BD交于E点,根据正弦的定义得到AH=AE•sinθ,PC=CE•sin∠PEC=CE•sinθ,然后再根据三角形面积公式得到S△ABD=
 AH•BD,S△CBD=
AH•BD,S△CBD= CP•BD,再把两个三角形面积相加即可得到四边形ABCD的面积S=
CP•BD,再把两个三角形面积相加即可得到四边形ABCD的面积S= m•n•sinθ.
m•n•sinθ.点评:本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了三角形面积公式.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目

 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是 如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是________.
如图,EF过平行四边形ABCD的对角形的交点O,交AD于点E,交BC于点F,已知AB=5,BC=6,OE=2,那么四边形EFCD的周长是________.