题目内容
11.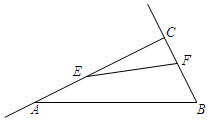 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm,点E从点C出发沿射线CA以每秒2cm的速度运动,同时点F从点B出发沿射线BC以每秒1cm的速度运动.设运动时间为t秒.
(1)填空:AB=4$\sqrt{5}$cm;
(2)若0<t<4,试问:t为何值时,以E、C、F为顶点的三角形与△ABC相似;
(3)若∠ACB的平分线CG交△ECF的外接圆于点G.试探究在整个运动过程中,CE、CF、CG之间存在的数量关系,并说明理由.
分析 (1)利用勾股定理即可求得AB的长度;
(2)0<t<4时,E和F分别在边AC和BC上,分成△EFC∽△ABC和△FEC∽△ABC两种情况,根据相似三角形的对应边的比相等即可求解;
(3)分成0<t<4和t≥4两种情况进行讨论,当0<t<4时,证明△EGH≌△FGC,△CGH是等腰直角三角形,利用勾股定理即可求解,当t≥4时,思路相同.
解答 解:(1)在Rt△ACB中,∵∠C=90°,AC=8cm,BC=4cm,
∴AB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$
故答案为4$\sqrt{5}$.
(2)由题意,EC=2t,BF=t,FC=4-t
∵∠ECF=∠ACB,∴以E、C、F为顶点的三角形与△ACB相似有两种情况: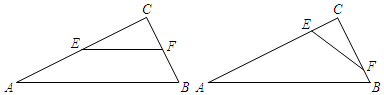
当$\frac{EC}{AC}$=$\frac{FC}{BC}$时,△EFC∽△ABC
∴$\frac{2t}{8}$=$\frac{4-t}{4}$,解得t=2,
当$\frac{EC}{BC}$=$\frac{FC}{AC}$时,△FEC∽△ABC
∴$\frac{2t}{4}$=$\frac{4-t}{8}$,解得t=0.8,
∴当t=0.8或2秒时,以E、C、F为顶点的三角形与△ABC相似.
(3)当0<t<4时,过点G作GH⊥CG交AC于H.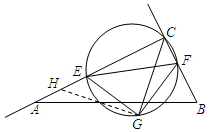
∵∠ACB=90°,
∴EF为△ECF的外接圆的直径,
∴∠EGF=90°,
∴∠HGC=∠EGF=90°
∴∠EGH=∠FGC
∵CG平分∠ACB,
∴∠ECG=∠FCG=45°
∴$\widehat{EG}$=$\widehat{FG}$,
∴EG=FG
∵∠ECG=45°,
∴∠EHG=45°
∴∠EHG=∠FCG,
∴△EGH≌△FGC
∴EH=FC
∵∠EHG=∠ECG=45°,
∴CH=$\sqrt{2}$CG
∵CH=CE+EH,
∴CE+CF=$\sqrt{2}$CG.
当t≥4时,过点G作GM⊥CG交AC于M.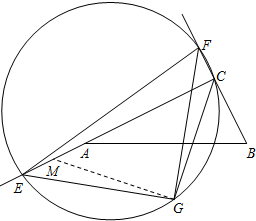
同理可得CE-CF=$\sqrt{2}$CG.
点评 本题考查全等三角形的判定与性质、勾股定理以及圆的弧、弦、圆心角、圆周角之间的关系等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案| A. | 6.96×103 | B. | 6.96×104 | C. | 6.96×105 | D. | 0.696×106 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. |  | B. |  | C. |  | D. |  |
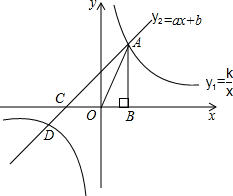 如图,已知反比例函数${y_1}=\frac{k}{x}$和一次函数y2=ax+b的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.求反比例函数和一次函数的解析式.
如图,已知反比例函数${y_1}=\frac{k}{x}$和一次函数y2=ax+b的图象相交于点A和点D,且点A的横坐标为1,点D的纵坐标为-1.过点A作AB⊥x轴于点B,△AOB的面积为1.求反比例函数和一次函数的解析式. 如图,⊙A的圆心A在反比例函数y=$\frac{3}{x}$(x>0)的图象上,且与x轴、y轴相切于点B、C,一次函数y=$\frac{{\sqrt{3}}}{3}$x+b的图象经过点C,且与x轴交于点D,与⊙A的另一个交点为点E.
如图,⊙A的圆心A在反比例函数y=$\frac{3}{x}$(x>0)的图象上,且与x轴、y轴相切于点B、C,一次函数y=$\frac{{\sqrt{3}}}{3}$x+b的图象经过点C,且与x轴交于点D,与⊙A的另一个交点为点E.