题目内容
如图8,在等腰梯形ABCD中,AD∥BC.O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H.已知⊙O与AB边相切,切点为F.
(1)求证:OE∥AB;
(2)求证:EH=![]() AB;
AB;
(3)若![]() ,
,![]() ,求⊙O的半径.
,求⊙O的半径.

解:(1) 证明:在等腰梯形ABCD中,AD∥BC.
∴![]() AB=DC,∠B=∠C
AB=DC,∠B=∠C
∵ OE=OC
∴∠OEC=∠C
∴∠B=∠OEC
∴OE∥AB
(2) 证明:连结OF,
∵⊙O与AB切于点F ,
 ∴OF⊥AB,
∴OF⊥AB,
∵EH⊥AB
∴OF ∥EH
又∵OE∥AB
∴四边形OEHF为平行四边形
∴EH= OF
∵OF=![]() CD=
CD=![]() AB
AB
∴EH=![]() AB
AB
(3)解:连结DE,设⊙O的半径为r,
∵CD是⊙O的直径,
∴∠DEC=90°
则∠DEC=∠EHB
又∵∠B=∠C
∴△EHB∽△DEC
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
在![]() 中,
中,![]()
∴![]() ,
,![]()
解得:![]()
![]()
∴⊙O的半径为![]()

练习册系列答案
相关题目
 条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
条件时,其一定平分梯形的面积?(只要求说出条件,不需证明)
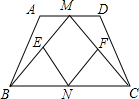 (2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题:
(2009•黔南州)杨老师在上四边形时给学生出了这样一个题.如图,若在等腰梯形ABCD中,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点时.提出以下问题: