题目内容
【题目】已知:抛物线y= ![]() (x﹣1)2﹣3.
(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
【答案】
(1)解:抛物线y= ![]() (x﹣1)2﹣3,
(x﹣1)2﹣3,
∵a= ![]() >0,
>0,
∴抛物线的开口向上,
对称轴为直线x=1;
(2)解:∵a= ![]() >0,
>0,
∴函数y有最小值,最小值为﹣3;
(3)解:令x=0,则y= ![]() (0﹣1)2﹣3=﹣
(0﹣1)2﹣3=﹣ ![]() ,
,
所以,点P的坐标为(0,﹣ ![]() ),
),
令y=0,则 ![]() (x﹣1)2﹣3=0,
(x﹣1)2﹣3=0,
解得x1=﹣1,x2=3,
所以,点Q的坐标为(﹣1,0)或(3,0),
当点P(0,﹣ ![]() ),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
),Q(﹣1,0)时,设直线PQ的解析式为y=kx+b(k≠0),
则 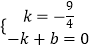 ,
,
解得 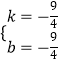 ,
,
所以直线PQ的解析式为y=﹣ ![]() x﹣
x﹣ ![]() ,
,
当P(0,﹣ ![]() ),Q(3,0)时,设直线PQ的解析式为y=mx+n,
),Q(3,0)时,设直线PQ的解析式为y=mx+n,
则 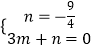 ,
,
解得 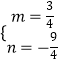 ,
,
所以,直线PQ的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
综上所述,直线PQ的解析式为y=﹣ ![]() x﹣
x﹣ ![]() 或y=
或y= ![]() x﹣
x﹣ ![]() .
.
【解析】(1)根据二次函数的性质,写出开口方向与对称轴即可;(2)根据a是正数确定有最小值,再根据函数解析式写出最小值;(3)分别求出点P、Q的坐标,再根据待定系数法求函数解析式解答.
【考点精析】通过灵活运用确定一次函数的表达式和二次函数的性质,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】下表反映了x与y之间存在某种函数关系,现给出了几种可能的函数关系式: y=x+7,y=x﹣5,y=﹣ ![]() ,y=
,y= ![]() x﹣1
x﹣1
x | … | ﹣6 | ﹣5 | 3 | 4 | … |
y | … | 1 | 1.2 | ﹣2 | ﹣1.5 | … |
(1)从所给出的几个式子中选出一个你认为满足上表要求的函数表达式:;
(2)请说明你选择这个函数表达式的理由.