Question

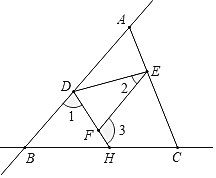
【题目】如图，直线AB和直线BC相交于点B，连接AC，点D、E、H分别在AB、AC、BC上，连接DE、DH，F是DH上一点,已知∠1+∠3=180°.

(1)求证:∠CEF=∠EAD；

(2)若DH平分∠BDE，∠2=求∠3的度数(用含的代数式表示).

Answer 1

【答案】（1）证明见解析，（2）∠3=90°+α.

【解析】

（1）根据平行线的判定和性质解答即可；
（2）根据平行线的性质解答即可．

解：（1）∵∠3+∠DFE=180°，∠1+∠3=180°
∴∠DFE=∠1，
∴AB∥EF，
∴∠CEF=∠EAD；
（2）∵AB∥EF，
∴∠2+∠BDE=180°
又∵∠2=α
∴∠BDE=180°-α
又∵DH平 分∠BDE
∴∠1=∠BDE=（180°-α）
∴∠3=180°-（180°-α）=90°+α