题目内容
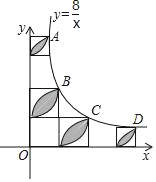
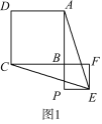
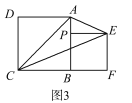
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 是线段
是线段![]() 上一点,将
上一点,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,且满足
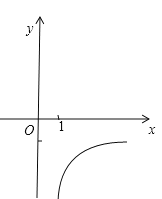
,且满足![]() . 若反比例函数
. 若反比例函数![]() 图象经过点
图象经过点![]() ,则
,则![]() 的值为____.
的值为____.

【答案】![]()
【解析】
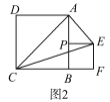
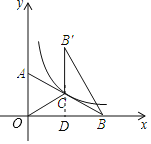
根据待定系数法求得直线AB的解析式y=﹣![]() x+2,延长B′C交OB于D,根据平行线的性质和轴对称的性质证得OC=BC=OA=2,设C点的坐标为(x,﹣
x+2,延长B′C交OB于D,根据平行线的性质和轴对称的性质证得OC=BC=OA=2,设C点的坐标为(x,﹣![]() x+2),则OD=x,B′D=﹣
x+2),则OD=x,B′D=﹣![]() x+4,由∠BOC=∠BB′C,cos∠COD=
x+4,由∠BOC=∠BB′C,cos∠COD=![]() ,cos∠BB′C=
,cos∠BB′C=![]() ,证得
,证得![]() ,即
,即![]() ,解得x=
,解得x=![]() ,即可求得C(
,即可求得C(![]() ,1),代入y=
,1),代入y=![]() (k>0)看求得k的值.
(k>0)看求得k的值.
设直线AB的解析式为:y=kx+b,
∵A(0,2),B(2![]() ,0),
,0),
∴![]() ,解得
,解得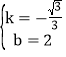 ,
,
∴直线AB的解析式为:y=﹣![]() x+2,
x+2,
延长B′C交OB于D,
∵A(0,2),B(2![]() ,0),
,0),
∴OA=2,OB=BB′=2![]() ,
,
∵B'C∥AO.
∴∠OAC=∠ACB,B′D⊥OB,
∵∠ACB=∠ACO,
∴∠OAC=∠OCA,
∴OC=B′C=OA=2,
∵点C是线段AB上一点,
∴设C(x,﹣![]() x+2),
x+2),
∴OD=x,B′D=2﹣![]() x+2=﹣
x+2=﹣![]() x+4,
x+4,
∵∠BOC=∠BB′C,cos∠COD=![]() ,cos∠BB′C=
,cos∠BB′C=![]()
∴![]() ,即
,即![]() ,
,
解得x=![]() ,
,
∴C(![]() ,1),
,1),
∵反比例函数y=![]() (k>0)图象经过点C,
(k>0)图象经过点C,
∴k=![]() ×1=
×1=![]() .
.
故答案是:![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目