Question

【题目】如图，面积为24的正方形ABCD中，有一个小正方形EFGH，其中E、F、G分别在AB、BC、FD上．若BF= ，则小正方形的周长为（ ）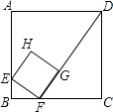
A.
B.
C.
D.

Answer 1

【答案】C
【解析】解：∵四边形ABCD是正方形，面积为24， ∴BC=CD=2 ，∠B=∠C=90°，
∵四边形EFGH是正方形，
∴∠EFG=90°，
∵∠EFB+∠DFC=90°，∠BEF+∠EFB=90°，
∴∠BEF=∠DFC，∵∠EBF=∠C=90°，
∴△BEF∽△CFD，
∴ = ，
∵BF= ，CF= ，DF= = ，
∴ = ，
∴EF= ，
∴正方形EFGH的周长为 ．
故选C．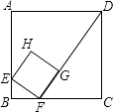

先利用勾股定理求出DF，再根据△BEF∽△CFD，得 = 求出EF即可解决问题．