题目内容
甲、乙两同学分别解同一道一元二次方程,甲把一次项系数看错了,而解得方程的两根为-2和3,乙把常数项看错了,解得两根为1+
和1-
,则原方程是( )
| 3 |
| 3 |
| A、x2-2x+6=0 |
| B、x2-2x-6=0 |
| C、x2+2x+6=0 |
| D、x2+2x-6=0 |
分析:先设这个方程的两根是α、β,由于甲把一次项系数看错了,而解得方程的两根为-2和3,则有αβ=
=-6,
乙把常数项看错了,解得两根为1+
和1-
,则有α+β=-
=2,令a=1,那么关于α、β的一元二次方程就是可求.
| c |
| a |
乙把常数项看错了,解得两根为1+
| 3 |
| 3 |
| b |
| a |
解答:解:设此方程的两个根是α、β,根据题意得
α+β=-
=2,αβ=
=-6,
令a=1,那么关于α、β的一元二次方程是x2-2x-6=0.
故选B.
α+β=-
| b |
| a |
| c |
| a |
令a=1,那么关于α、β的一元二次方程是x2-2x-6=0.
故选B.
点评:此题主要考查了根与系数的关系,若x1、x2是方程ax2+bx+c=0的两根,则有x1+x2=-
,x1x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
相关题目
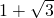 和
和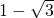 ,则原方程是
,则原方程是