题目内容
方程
的解是________．
x1=0，x2=2
分析：观察可知，先设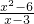
=y，原方程可变为y+
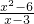=7，解出y，再代入=y，再次解方程即可．
解答：设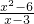=y，得
y+=7，
解得
y1=2，y2=5，
由于y1、y2≠0，故y1、y2都是y+=7的解，
把y1=2代入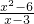=y中，可得
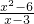=2，
解得x1=0，x2=2，
检验：把x1=0代入x-3=-3≠0，
把x2=2代入x-3=2-3=-1≠0，
∴x1=0、x2=2是原方程的解；
把y2=5代入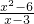=y中，可得
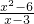=5，
化简得x2-5x+9=0，
而△=b2-4ac=-11＜0，
∴此方程无解．
故原方程的解是x1=0，x2=2．
故答案是x1=0，x2=2．
点评：本题考查了解分式方程．
（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．
（2）解分式方程一定注意要验根．
分析：观察可知，先设
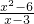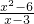=y，原方程可变为y+=7，解出y，再代入=y，再次解方程即可．解答：设
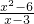=y，得y+
=7，解得
y1=2，y2=5，
由于y1、y2≠0，故y1、y2都是y+
=7的解，把y1=2代入
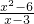=y中，可得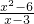=2，解得x1=0，x2=2，
检验：把x1=0代入x-3=-3≠0，
把x2=2代入x-3=2-3=-1≠0，
∴x1=0、x2=2是原方程的解；
把y2=5代入
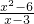=y中，可得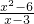=5，化简得x2-5x+9=0，
而△=b2-4ac=-11＜0，
∴此方程无解．
故原方程的解是x1=0，x2=2．
故答案是x1=0，x2=2．
点评：本题考查了解分式方程．
（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．
（2）解分式方程一定注意要验根．
练习册系列答案
轻松暑假总复习系列答案
相关题目
某二元方程的解是
，若把x看作平面直角坐标系中点的横坐标，y看作平面直角坐标系中点的纵坐标，下面说法正确的是（ ）
|
| A、点（x，y）一定不在第一象限 |
| B、点（x，y）一定不是坐标原点 |
| C、y随x的增大而增大 |
| D、y随x的增大而减小 |