题目内容
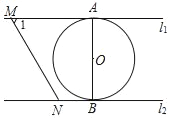
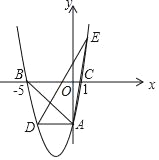
【题目】如图,在平面直角坐标系![]() 中,顶点为
中,顶点为![]() 的抛物线
的抛物线![]() :
:![]() (
(![]() )经过点
)经过点![]() 和
和![]() 轴上的点
轴上的点![]() ,
,![]() ,
,![]() .
.
(1)求该抛物线的表达式;
(2)联结![]() ,求
,求![]() ;
;
(3)将抛物线![]() 向上平移得到抛物线
向上平移得到抛物线![]() ,抛物线
,抛物线![]() 与
与![]() 轴分别交于点
轴分别交于点![]() (点
(点![]() 在点
在点![]() 的左侧),如果
的左侧),如果![]() 与
与![]() 相似,求所有符合条件的抛物线
相似,求所有符合条件的抛物线![]() 的表达式.
的表达式.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)抛物线
;(3)抛物线![]() 为:
为:![]() 或
或![]() .
.
【解析】
(1)根据题意,可以写出点B和点A的坐标,从而可以得到该抛物线的表达式;
(2)根据(1)中的函数解析式,可以求得点M的坐标,从而可以求得直线AM的函数解析式,从而可以求得S△AOM;
(3)根据题意,利用分类讨论的方法和三角形相似的知识可以求得点F的坐标,从而可以求得抛物线C2的表达式.
解:(1)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵![]() ,∴
,∴![]()
∵![]()
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]()
∵抛物线![]() :
:![]() 经过点
经过点![]() ,
,
∴可得: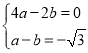 ,
,
解得: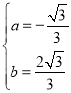
∴这条抛物线的表达式为![]() ;
;
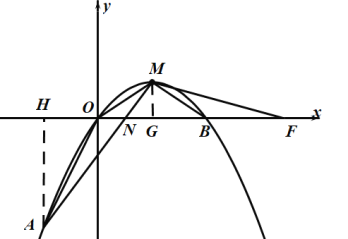
(2)过![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵![]() =
=![]()
∴顶点![]() 是
是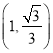 ,得
,得![]()
设直线AM为y=kx+b,
把![]() ,
,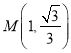 代入得
代入得 ,解得
,解得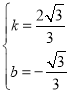
∴直线![]() 为
为![]()
令y=0,解得x=![]()
∴直线![]() 与
与![]() 轴的交点
轴的交点![]() 为
为![]()
∴![]()
(3)∵![]() 、
、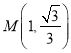 ,
,
∴在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() .由抛物线的轴对称性得:
.由抛物线的轴对称性得:![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]()
∴![]() .
.
∴当![]() 与
与![]() 相似时,有:
相似时,有:![]() 或
或![]()
即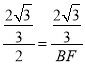 或
或 ,
,
∴![]() 或
或![]() .
.
∴![]() 或
或![]()
设向上平移后的抛物线![]() 为:
为:![]() ,
,
当![]() 时,
时,![]() ,
,
∴抛物线![]() 为:
为:![]()
当![]() 时,
时,![]() ,
,
∴抛物线![]() 为:
为:![]() .
.
综上:抛物线![]() 为:
为:![]() 或
或![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目