题目内容
【题目】如图,直线y=2x+4与反比例函数y= ![]() 的图象相交于A(﹣3,a)和B两点
的图象相交于A(﹣3,a)和B两点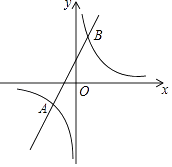
(1)求k的值;
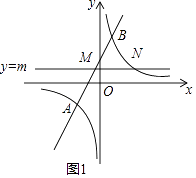
(2)直线y=m(m>0)与直线AB相交于点M,与反比例函数的图象相交于点N.若MN=4,求m的值;
(3)直接写出不等式 ![]() >x的解集.
>x的解集.
【答案】
(1)∵点A(﹣3,a)在y=2x+4与y= ![]() 的图象上,
的图象上,
∴2×(﹣3)+4=a,
∴a=﹣2,
∴k=(﹣3)×(﹣2)=6;
(2)∵M在直线AB上,
∴M( ![]() ,m),N在反比例函数y=
,m),N在反比例函数y= ![]() 上,
上,
∴N( ![]() ,m),
,m),
∴MN=xN﹣xM= ![]() ﹣
﹣ ![]() =4或xM﹣xN=
=4或xM﹣xN= ![]() ﹣
﹣ ![]() =4,
=4,
解得:∵m>0,
∴m=2或m=6+4 ![]() ;
;
(3)x<﹣1或5<x<6,
由 ![]() >x得:
>x得: ![]() ﹣x>0,
﹣x>0,
∴ ![]() >0,
>0,
∴ ![]() <0,
<0,
∴ ![]() 或
或 ![]() ,
,
结合抛物线y=x2﹣5x﹣6的图象可知,由 ![]() 得
得
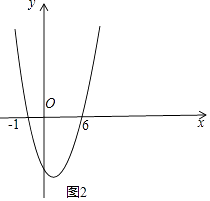
![]() ,
,
∴ ![]() 或
或 ![]() ,
,
∴此时x<﹣1,
由 ![]() 得,
得, ![]() ,
,
∴ ![]() ,
,
解得:5<x<6,
综上,原不等式的解集是:x<﹣1或5<x<6.
【解析】(1)把点A(﹣3,a)分别代入y=2x+4与y=![]() 中,即可求出k;(2)由M、N点均在双曲线上,用m的代数式表示两点坐标,根据MN=4,即
中,即可求出k;(2)由M、N点均在双曲线上,用m的代数式表示两点坐标,根据MN=4,即
xN-xM=4,建立方程求出m;(3)变形不等式![]() ,即
,即![]() ,分两种情况讨论:
,分两种情况讨论:![]() 或
或![]() ,运用数形结合的思想,画出y=
,运用数形结合的思想,画出y=![]() 的图象,找出与x轴交点的横坐标,即可求出.
的图象,找出与x轴交点的横坐标,即可求出.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目