题目内容
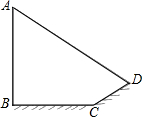 如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为
如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为| 2 |
| 3 |
分析:先根据CD的长以及坡角求出落在斜坡上的影长在地面上的实际长度,即可知AB的总影长,然后根据1 m杆的影子长为2 m,求解电线杆的高度.
解答:解:作DE⊥BC于E.则电线杆的高度分3部分进行求解.
BC对应的电线杆的高度:根据同一时刻物高与影长成比例,得10÷2=5;
在Rt△CDE中,根据30°所对的直角边是斜边的一半,得DE=2.再根据勾股定理,得CE=2
;
因为DE⊥BC,则DE对应的电线杆高度和DE相等,CE对应的电线杆高度同样根据:同一时刻物高与影长成比例,
是2
÷2=
.
故电线杆的高度是5+2+
≈8.7.

BC对应的电线杆的高度:根据同一时刻物高与影长成比例,得10÷2=5;
在Rt△CDE中,根据30°所对的直角边是斜边的一半,得DE=2.再根据勾股定理,得CE=2
| 3 |
因为DE⊥BC,则DE对应的电线杆高度和DE相等,CE对应的电线杆高度同样根据:同一时刻物高与影长成比例,
是2
| 3 |
| 3 |
故电线杆的高度是5+2+
| 3 |
点评:注意:影子平行于物体时,影子和物体的实际高度相等;影子垂直于物体时,根据同一时刻物高与影长成比例进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字,
如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字, ≈1.41,
≈1.41, ≈1.73)
≈1.73) 如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字,
如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字, ≈1.41,
≈1.41, ≈1.73)
≈1.73) 如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字,
如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字, ≈1.41,
≈1.41, ≈1.73)
≈1.73)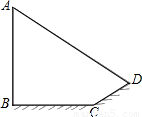 (2010•鞍山)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字,
(2010•鞍山)如图小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为 m.(结果保留两位有效数字, ≈1.41,
≈1.41,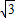 ≈1.73)
≈1.73)