题目内容
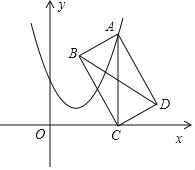
【题目】如图,抛物线y=﹣ ![]() x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC=
x2+bx+c与y轴交于点C,与x轴交于A、B两点(点A在原点左侧,点B在原点右侧),且∠ACB=90°,tan∠BAC= ![]() .
.
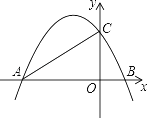
①求抛物线的解析式;
②若抛物线顶点为P,求四边形APCB的面积.
【答案】①y=﹣ ![]() x2﹣
x2﹣ ![]() x+ 2;②
x+ 2;②![]() .
.
【解析】
①由y=-![]() x2+bx+c=c,可求得C(0,c),由tan∠BAC=
x2+bx+c=c,可求得C(0,c),由tan∠BAC=![]() ,可设A(-2c,0),B(
,可设A(-2c,0),B(![]() c,0),把A(-2c,0),B(
c,0),把A(-2c,0),B(![]() c,0)代入y=-
c,0)代入y=-![]() x2+bx+c=c求得b,c,即可求得求抛物线的解析式;
x2+bx+c=c求得b,c,即可求得求抛物线的解析式;
②解方程-![]() x2-
x2-![]() x+
x+![]() =0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB,根据三角形的面积公式即可求得结论.
=0可求得A,B点的坐标,由于四边形APCB的面积=S△AOP+S△POC+S△COB,根据三角形的面积公式即可求得结论.
①令x=0则y=﹣![]() x2+bx+c=c,
x2+bx+c=c,
∴C(0,c),
∵tan∠BAC=![]() ,
,
∴A(﹣2c,0),
∠ACB=90°,
∴∠BCO=∠BAC,
∴OB=![]() OC=
OC=![]() c,
c,
∴B(![]() c,0),
c,0),
把A(﹣2c,0),B( ![]() c,0)代入y=﹣
c,0)代入y=﹣![]() x2+bx+c=c,
x2+bx+c=c,
得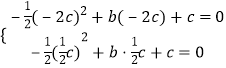 ,
,
解得: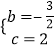 ,
,
求抛物线的解析式为y=﹣![]() x2﹣
x2﹣![]() x+ 2;
x+ 2;
②y=﹣![]() x2﹣
x2﹣![]() x+2=﹣
x+2=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴P(﹣![]() ,
,![]() ),
),
令﹣![]() x2﹣
x2﹣![]() x+2=0,解得:x1=﹣1,x2=
x+2=0,解得:x1=﹣1,x2=![]() ,
,
∴A(﹣4,0),B( 1,0)
连接AP,PC,CB,PO,则四边形APCB的面积=S△AOP+S△POC+S△COB=![]() ×4×
×4×![]() +
+![]() ×2×
×2×![]() +
+![]() ×1×2=
×1×2=![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目