题目内容
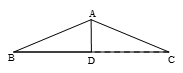
如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则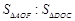 = .
= .
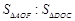 = .
= .
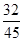 .
.试题分析:如图,作DG⊥AB于G,DH⊥AC与H,设AD=x,则BD=3x,由勾股定理就可以求出AB=
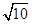 x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.解答:解:作DG⊥AB于G,DH⊥AC与H,
x,由三角形的面积公式求出DG的值,由三角函数值求出AG,就可以表示出AE,从而求出AF,再由△AFO∽△DCO就可以求出结论.解答:解:作DG⊥AB于G,DH⊥AC与H,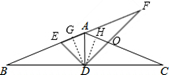
∵AB=AC,AD⊥BC,
∴∠ADB=∠ADC=90°,∠BAD=∠CAD,∠B=∠C.
∴DG=DH.
设设AD=x,则BD=3x,由勾股定理,得
AB=
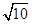 x,
x,∴AC=
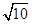 x.
x.∴
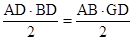 ,
,∴
 ,
,∴GD=
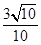 .
.∵
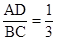 =tan∠C.
=tan∠C.∴tan∠B=
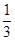 .
.∵∠ADG+∠GAD=90°,∠B+∠GAD=90°,
∴∠ADG=∠B.
∴tan∠ADG=
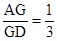 ,
,∴
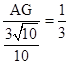 ,
,∴AG=
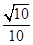 x.
x.∵△FDE是由△CDA旋转得来的,
∴△FDE≌△CDA,
∴DE=DA.∠F=∠C.
∵DG⊥AB,
∴AG=EG.
∴AE=2AG,
∴AE=
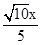 .
.∴AF=
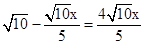 .
.∵∠AOF=∠DOC,∠F=∠C,
∴△AFO∽△DCO,
∴S△AOF:S△DOC=
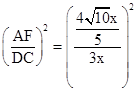 =
=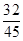 .
.故答案为:
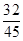 .
.
练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
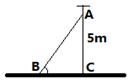
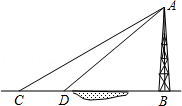
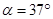 ,工作人员需买拉线的长度约为_______(精确到米)。(
,工作人员需买拉线的长度约为_______(精确到米)。(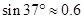 ,
,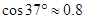 )
)


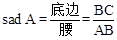 . 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义,解下列问题:
. 我们容易知道一个角的大小与这个角的正对值也是互相唯一确定的.根据上述角的正对定义,解下列问题: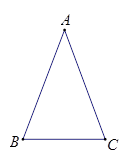
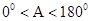 ,
,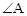 的正对值sadA的取值范围是_____________。
的正对值sadA的取值范围是_____________。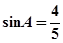 ,则
,则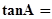 ( ).
( ). 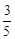
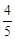
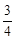
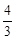
 为一锐角,且
为一锐角,且 ,则
,则 .
.