题目内容
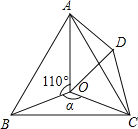
【题目】如图，四边形ABCD中，∠A＝∠C＝90°，∠ABC＝135°，CD＝6，AB＝2，则四边形ABCD的面积为___________
【答案】16
【解析】
延长AB和DC，两线交于O，求出OB=
BC，OD=OA，OA=AD，BC=OC，设BC=OC=x，则BO=x，解直角三角形得出方程，求出x，再分别求出△AOD和△BOC的面积即可．
延长AB和DC，两线交于O，
∵∠C=90°，∠ABC=135°，
∴∠OBC=45°，∠BCO=90°，
∴∠O=45°，
∵∠A=90°，
∴∠D=45°，
则OB=BC，OD=OA，OA=AD，BC=OC，
设BC=OC=x，则BO=x，
∵CD=6，AB=2，
∴6+x=（x+2），
解得：x=6-2，
∴OB=6-4，BC=OC=6-2，OA=AD=2+6-4=6-2，
∴S四边形ABCD=S△OAD-S△OBC
=
OAAD-BCOC
=
=16，
故答案为：16．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
