题目内容
 如图,点A、B在⊙O上,∠AOB=90°.OA=2,AC=CB,CD∥AO交⊙O于点D,则CD的长是
如图,点A、B在⊙O上,∠AOB=90°.OA=2,AC=CB,CD∥AO交⊙O于点D,则CD的长是
- A.1
- B.

- C.

- D.

C
分析:DC延长交OB于点E,根据平行线的性质得到∠DEO=∠AOB=90°,根据平行线分线段成比例定理求出OE、CE,根据勾股定理求出DE根据CD=DE-CE即可求出答案.
解答: 解:延长DC,交OB于点E,
解:延长DC,交OB于点E,
∵CD∥OA,∠AOB=90°,
∴∠DEO=∠AOB=90°,
∵OD=OA=2,
C是线段AB中点,
∴CE是△AOB的中位线,
∴OE=EB=1,
根据勾股定理得:DE= ,
,
CE= OA=1,
OA=1,
∴CD=DE-CE= -1
-1
故选C.
点评:本题主要考查对平行线的性质,勾股定理,平行线分线段成比例定理等知识点的理解和掌握,能求出DE、CE的长是解此题的关键.
分析:DC延长交OB于点E,根据平行线的性质得到∠DEO=∠AOB=90°,根据平行线分线段成比例定理求出OE、CE,根据勾股定理求出DE根据CD=DE-CE即可求出答案.
解答:
 解:延长DC,交OB于点E,
解:延长DC,交OB于点E,∵CD∥OA,∠AOB=90°,
∴∠DEO=∠AOB=90°,
∵OD=OA=2,
C是线段AB中点,
∴CE是△AOB的中位线,
∴OE=EB=1,
根据勾股定理得:DE=
 ,
,CE=
 OA=1,
OA=1,∴CD=DE-CE=
 -1
-1故选C.
点评:本题主要考查对平行线的性质,勾股定理,平行线分线段成比例定理等知识点的理解和掌握,能求出DE、CE的长是解此题的关键.

练习册系列答案
相关题目


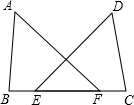 如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
如图,点E、F在BC上,AB=DC,∠B=∠C,∠A=∠D,
 如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为
如图,点C、D在线段AB上,且C为AB的一个四等分点,D为AC中点,若BC=2,则BD的长为