题目内容
已知直角三角形两条直角边的长是5和12,则其外接圆的半径是________.

分析:先根据勾股定理求出直角三角形斜边的长,再根据其外接圆的半径是斜边的一半即可得出结论.
解答:∵直角边长分别为5和12,
∴斜边长=
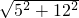 =13,
=13,∴这个直角三角形的外接圆的半径=
 .
.故答案为:
 .
.点评:本题考查的是三角形的外接圆与外心及勾股定理,熟知直角三角形的外接圆的半径是其斜边的一半是解答此题的关键.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
题目内容

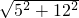 =13,
=13, .
. .
.
 小题狂做系列答案
小题狂做系列答案