题目内容
如图，将矩形纸片ABCD沿EF折叠，使点A落在DC边上的点A′处，x轴垂直平分D
A，直线EF的表达式为y=kx-k（k＜0））
（1）问：EF与抛物线y=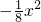
有几个公共点？
（2）当EF与抛物线只有一个公共点时，设A′（x，y），求
的值．
解：（1）由
，得x2+8kx-8k=0，
△=（8k）2+32k=32k（2k+1），
∵k＜0．
∴
，EF与抛物线有两个公共点，
当
时，EF与抛物线有一个公共点，
当
时，EF与抛物线没有公共点，
（2）EF与抛物线只有一个公共点时，
，EF的表达式为
，
EF与x轴、y轴的交点为M（1，0），E（0，
），
∵∠EMO=90°-∠OEM=∠EAA′，
∴RT△EMO∽RT△A′AD
∴
，
∴
．
分析：（1）根据判别式与坐标轴交点个数性质，分别得出即可；
（2）首先得出EF与x轴、y轴的交点为M（1，0），E（0，），进而得出RT△EMO∽RT△A′AD，即可求出．
点评：此题主要考查了判别式与图象与x轴交点个数的规律以及三角形相似的判定方法，三角形相似经常与二次函数相结合同学们应有意识地运用．
，得x2+8kx-8k=0，△=（8k）2+32k=32k（2k+1），
∵k＜0．
∴
，EF与抛物线有两个公共点，当
时，EF与抛物线有一个公共点，当
时，EF与抛物线没有公共点，（2）EF与抛物线只有一个公共点时，
，EF的表达式为，EF与x轴、y轴的交点为M（1，0），E（0，
），∵∠EMO=90°-∠OEM=∠EAA′，
∴RT△EMO∽RT△A′AD
∴
，∴
．分析：（1）根据判别式与坐标轴交点个数性质，分别得出即可；
（2）首先得出EF与x轴、y轴的交点为M（1，0），E（0，
），进而得出RT△EMO∽RT△A′AD，即可求出．点评：此题主要考查了判别式与图象与x轴交点个数的规律以及三角形相似的判定方法，三角形相似经常与二次函数相结合同学们应有意识地运用．
练习册系列答案
相关题目
23、如图，将矩形纸片ABCD沿EF折叠，使点A与点C重合，点D落在点G处，EF为折痕．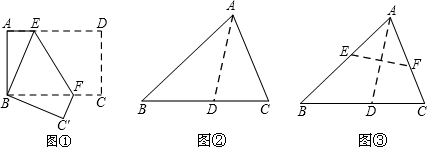
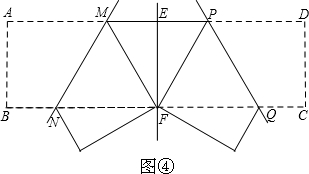
（2013•松北区三模）如图，将矩形纸片ABCD折痕，使点D落在点线段AB的中点F处．若AB=4，则边BC的长为（ ）
如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．
