Question

(2006安徽，23)(13分)取一副三角板按图①拼接，固定三角板ADC，将三板ABC绕点A依顺时针方向旋转一个大小为α的角(0°＜α≤45°)得到△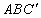，如图所示．

试问：(1)当α为多少度时，能使得图②中AB∥DC？

(2)当旋转到图③位置，此时α又为多少度？图③中你能找出哪几对相似三角形，并求其中一对的相似比；

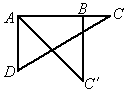
图③

(3)连结BD，当0°＜α≤45°时，探寻∠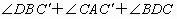值的大小变化情况，并给出你的证明．

Answer 1

答案：略
解析：

(1)如图②，由题意∠，要使AB∥DC，须∠BAC=∠ACD，∴∠BAC=30°．45°－30°=15°即α=15°时，能使得AB∥DC．(4分) 图② (2)易得α=45°时，可得图③，此时，若记DC与、分别交于点E、F． 图③ 则共有两对相似三角形：ΔBFC∽ΔADC，Δ∽ΔADE．(6分) 下求ΔBFC与ΔADC的相似比： 在图③中，设AB=a，则易得AC=．则．(8分) 注：Δ与ΔADE的相似比为：． (3)解法一： 当0°＜α≤45°时，总有Δ存在． ∵，又=180°，∴=180°．(11分) 又∵=45°，∠C=30°，∴=105°．(13分)