题目内容
 已知:如图,AD∥BC,AC⊥BD于O,AD+BC=5,AC=3,AE⊥BC于E.求AE的长.
已知:如图,AD∥BC,AC⊥BD于O,AD+BC=5,AC=3,AE⊥BC于E.求AE的长.
分析:过点A作AF∥DB交CB延长线于F,通过辅助线,将已知条件与未知量联系起来,此时,AE是直角三角形斜边上的高,而已知斜边和一直角边,先由勾股定理求出另一直角边,再由面积法就可以求出斜边上的高AE了.
解答: 解:过点A作AF∥DB交CB的延长线于点F,(1分)
解:过点A作AF∥DB交CB的延长线于点F,(1分)
∵AD∥BC,
∴四边形AFBD是平行四边形.
∴FB=AD.
∵AD+BC=5,
∴FC=FB+BC=AD+BC=5.(2分)
∵AC⊥BD,
∴FA⊥AC.(3分)
在△FAC中,∠FAC=90°,AC=3,FC=5,
∴AF=4.(4分)
∵AE⊥BC于E,
∴AF•AC=FC•AE.
∴AE=
.(5分)
 解:过点A作AF∥DB交CB的延长线于点F,(1分)
解:过点A作AF∥DB交CB的延长线于点F,(1分)∵AD∥BC,
∴四边形AFBD是平行四边形.
∴FB=AD.
∵AD+BC=5,
∴FC=FB+BC=AD+BC=5.(2分)
∵AC⊥BD,
∴FA⊥AC.(3分)
在△FAC中,∠FAC=90°,AC=3,FC=5,
∴AF=4.(4分)
∵AE⊥BC于E,
∴AF•AC=FC•AE.
∴AE=
| 12 |
| 5 |
点评:当直接求解比较困难时,通常要作辅助线,将已知条件与未知量联系起来.

练习册系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.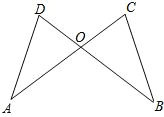 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.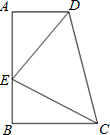 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC. 根据题意填空:
根据题意填空: