Question

（2012•沙河口区模拟）一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间t（h），两车之间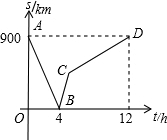的距离为s（km），图中的折线表示s与t之间的函数关系．根据图象进行以下探究：
（1）试解释图中点B的实际意义；
（2）①求线段BC所表示的s与t之间的函数关系式，并写出自变量t的取值范围；
②若第二列快车也从甲地出发驶往乙地，速度与第一列快车相同．在第一列快车与慢车相遇30分钟后，第二列快车与慢车相遇．求第二列快车比第一列快车晚出发多长时间？

Answer 1

分析：（1）根据点B出两车距离为0可知，两车相遇；
（2）①根据图象可知慢车从乙地到甲地的时间为12小时，然后求出慢车的速度，再根据相遇问题求出快车的速度，再点C出快车到达乙地，然后求出时间，即可得到点C的横坐标，再根据快车的速度求出点C的纵坐标，然后利用待定系数法求直线函数解析式解答即可；
②设晚出发x小时，然后表示出到相遇时慢车与第二列快车行驶的时间，再根据相遇时两车行驶的路程之和等于总路程列出方程，然后解方程即可．

解答：解：（1）图中点B的实际意义是：当慢车行驶4h时，慢车和快车相遇；

（2）慢车速度为900÷12=75km/h，
设快车速度为a，则4（a+75）=900，
解得a=150，
∵900÷150=6小时，
（150+75）×（6-4）=450千米，
∴点C的坐标为（6，450），
设线段BC的解析式为s=kt+b，
∵点B的坐标为（4，0），
∴

4k+b=0 6k+b=450

，
解得

k=225 b=-900

，
所以，线段BC所表示的函数关系式为：s=225t-900（4≤t≤6）；

（3）设第二列快车晚出发x小时，到相遇时，第二列快车行驶的时间是（4.5-x），慢车行驶的时间是4.5小时，
根据题意得，150×（4.5-x）+75×4.5=900，
解得x=0.75小时．
答：第二列快车比第一列快车晚出发0.75h．

点评：本题考查了一次函数的应用，相遇问题，待定系数法求一次函数解析式，根据图象信息，求出慢车的速度，然后根据相遇求出快车的速度是解题的关键．