题目内容
（2013•西宁）如图，AB为⊙O的直径，弦CD⊥AB于点E，若CD=6，且AE：BE=1：3，则AB=4
| 3 |
4
．| 3 |
分析：根据AE与BE比值，设出AE为x与BE为3x，由AE+BE表示出AB，进而表示出OA与OB，由OA-AE表示出OE，连接OC，根据AB与CD垂直，利用垂径定理得到E为CD中点，求出CE的长，在直角三角形OCE中，利用勾股定理列出方程，求出方程的解得到x的值，即可确定出AB的长．
解答：
解：连接OC，
根据题意设AE=x，则BE=3x，AB=AE+EB=4x，
∴OC=OA=OB=2x，OE=OA-AE=x，
∵AB⊥CD，∴E为CD中点，即CE=DE=
CD=3，
在Rt△CEO中，利用勾股定理得：（2x）2=32+x2，
解得：x=
，
则AB=4x=4
．
故答案为：4
解：连接OC，根据题意设AE=x，则BE=3x，AB=AE+EB=4x，
∴OC=OA=OB=2x，OE=OA-AE=x，
∵AB⊥CD，∴E为CD中点，即CE=DE=
| 1 |
| 2 |
在Rt△CEO中，利用勾股定理得：（2x）2=32+x2，
解得：x=
| 3 |
则AB=4x=4
| 3 |
故答案为：4
| 3 |
点评：此题考查了垂径定理，以及勾股定理，熟练掌握定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
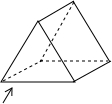（2013•西宁）如图所示的几何体的俯视图应该是（ ）
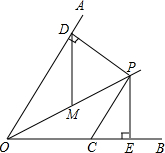（2013•西宁）如图，已知OP平分∠AOB，∠AOB=60°，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（ ）
（2013•西宁）如图，矩形的长和宽分别是4和3，等腰三角形的底和高分别是3和4，如果此三角形的底和矩形的宽重合，并且沿矩形两条宽的中点所在的直线自右向左匀速运动至等腰三角形的底与另一宽重合．设矩形与等腰三角形重叠部分（阴影部分）的面积为y，重叠部分图形的高为x，那么y关于x的函数图象大致应为（ ）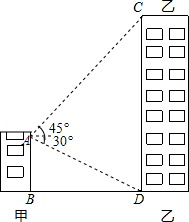
（2013•西宁）如图，甲乙两幢楼之间的距离是30米，自甲楼顶A处测得乙楼顶端C处的仰角为45°，测得乙楼底部D处的俯角为30°，则乙楼的高度为
（2013•西宁）如图，网格图中每个小正方形的边长为1，则弧AB的弧长l=