题目内容
 已知,如图,在△ABC中,AB=BC,BD是∠ABC的平分线,E为AB的中点,连接DE,求证:BE=DE.
已知,如图,在△ABC中,AB=BC,BD是∠ABC的平分线,E为AB的中点,连接DE,求证:BE=DE.考点:直角三角形斜边上的中线,等腰三角形的性质
专题:证明题
分析:根据等腰三角形三线合一的性质,得BD⊥AC,再根据直角三角形的斜边的中线等于斜边的一半即可证得.
解答:证明:∵在△ABC中,AB=BC,BD是∠ABC的平分线,
∴BD⊥AC,
又E是AB边的中点,
∴DE=
AB.
∵BE=
AB,
∴BE=DE.
∴BD⊥AC,
又E是AB边的中点,
∴DE=
| 1 |
| 2 |
∵BE=
| 1 |
| 2 |
∴BE=DE.
点评:此题综合考查了等腰三角形三线合一的性质和直角三角形的斜边的中线的性质.

练习册系列答案
相关题目
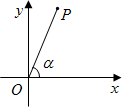 如图,在直角坐标系中,P是第一象限内的点,其坐标是(4,m),且OP与x轴正半轴的夹角α的余弦值是
如图,在直角坐标系中,P是第一象限内的点,其坐标是(4,m),且OP与x轴正半轴的夹角α的余弦值是| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若方程
=
+
有增根,则增根可能为( )
| 5 |
| x-2 |
| a |
| x |
| 4 |
| x(x-2) |
| A、0 | B、2 | C、0或2 | D、1 |
若2a-7与3a-3是同一个数的平方根,则a的值是( )
| A、-2 | B、-4 | C、2或-4 | D、2 |
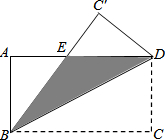 如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.
如图,在矩形ABCD中,AB=3,AD=5,现将该矩形沿对角线BD折叠,使得点C落在点C′处,BC′边交AD边于点E,请求出图中阴影部分的面积.