��Ŀ����
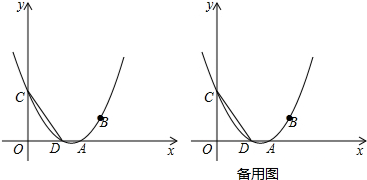
��2013•��ɽ��ģ����֪������y=ax2+bx+3��a��0������A��3��0����B��4��1�����㣬��x����һ����ΪD����y�ύ�ڵ�C��
��1����������y=ax2+bx+3��a��0���ĺ�����ϵʽ��
��2����ͼ������AC�������������Ƿ���ڵ�P��ʹ��ACD+��ACP=45�㣿�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3������AC��EΪ�߶�AC������һ�㣨����A��C�غϣ�����A��E��O�����Բ��ֱ��AB�ڵ�F��
�ٵ�E���˶��������ı���OEAF������Ƿ����仯����˵�����ɣ�
�ڵ�EF���ı���OEAF�����Ϊ1��2������ʱ�����E�����꣮
��1����������y=ax2+bx+3��a��0���ĺ�����ϵʽ��
��2����ͼ������AC�������������Ƿ���ڵ�P��ʹ��ACD+��ACP=45�㣿�����ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3������AC��EΪ�߶�AC������һ�㣨����A��C�غϣ�����A��E��O�����Բ��ֱ��AB�ڵ�F��
�ٵ�E���˶��������ı���OEAF������Ƿ����仯����˵�����ɣ�
�ڵ�EF���ı���OEAF�����Ϊ1��2������ʱ�����E�����꣮

��������1���ѵ�A��B��������뺯������ʽ�����ô���ϵ��������κ�������ʽ���
��2������D��DF��AC��F�����ݺ�������ʽ�����D�����꣬�Ӷ����AD�ij��������AC��AF��DF��Ȼ�����CF�ij������
��Ȼ����ݡ�ACD+��ACP=45�㣬���������ε�һ����ǵ������������ڵ������ڽǵĺ��Լ����������ζ�Ӧ����ȣ���x���ϵĵ�G��ʹ��OGC=��DCF��Ȼ�����ô���ϵ�������ֱ��CG�Ľ���ʽ����������������⼴�ɣ�
��3���ٸ��ݵ�A��B���������ֱ��AB��x��ļн���45�㣬�Ӷ��õ���OAF=��OCE���ٸ���Բ�ڽ��ı��ε����ʿɵá�OEC=��OFA��Ȼ�����á��ǽDZߡ�֤����OCE�͡�OAFȫ�ȣ��ٸ���ȫ�������ε�����������ı���OEAF��������AOC�������ȣ�Ȼ����ʽ���㼴�ɵý⣻
�ڷ���������OEF����������жϳ���OEF�ǵ���ֱ�������Σ�Ȼ�����������ε�������OE2���ٸ��ݵ�A��C���������ֱ��AC�Ľ���ʽΪy=-x+3��Ȼ�������E������Ϊ��a��-a+3����Ȼ�����ù��ɶ�����ʽ���㼴�ɵý⣮
��2������D��DF��AC��F�����ݺ�������ʽ�����D�����꣬�Ӷ����AD�ij��������AC��AF��DF��Ȼ�����CF�ij������
| DF |
| CF |
��3���ٸ��ݵ�A��B���������ֱ��AB��x��ļн���45�㣬�Ӷ��õ���OAF=��OCE���ٸ���Բ�ڽ��ı��ε����ʿɵá�OEC=��OFA��Ȼ�����á��ǽDZߡ�֤����OCE�͡�OAFȫ�ȣ��ٸ���ȫ�������ε�����������ı���OEAF��������AOC�������ȣ�Ȼ����ʽ���㼴�ɵý⣻
�ڷ���������OEF����������жϳ���OEF�ǵ���ֱ�������Σ�Ȼ�����������ε�������OE2���ٸ��ݵ�A��C���������ֱ��AC�Ľ���ʽΪy=-x+3��Ȼ�������E������Ϊ��a��-a+3����Ȼ�����ù��ɶ�����ʽ���㼴�ɵý⣮
����⣺��1����������y=ax2+bx+3��a��0������A��3��0����B��4��1�����㣬
��
��
���
��
�������ߵĹ�ϵʽΪy=
x2-
x+3��
��2������D��DF��AC��F��
��y=0����
x2-
x+3=0��
�����ã�x2-5x+6=0��
���x1=2��x2=3��
���D������2��0����AD=1��
��x=0����y=3��
���C������0��3����
��OC=OA=3��
���OAC�ǵ���ֱ�������Σ�
��AC=
=
=3
��
AF=DF=
��AD=
��
��CF=AC-AF=3
-
=
��
��
=
=
��
�ߡ�ACD+��ACP=45�㣬
����G��15��0����
��
=
=
��
CG�������ߵĽ���Ϊ��P��
��ֱ��CG�Ľ���ʽΪy=kx+b��
��
��
���
��
��y=-
x+3��
����
��
���
��
��Ϊ��C���꣬��ȥ����
���P������
��
����
��3���١�A��3��0����B��4��1����
��ֱ��AB��x��ļн�Ϊ45�㣬
���OAF=45�㣬
���OAF=��OCE=45�㣬
���ı���OEAF��Բ�ڽ��ı��Σ�
���OEC=��OFA��
�ڡ�OCE�͡�OAF�У�
��
���OCE�ա�OAF��AAS����
��S��OCE=S��OAF��
���ı���OEAF�����=��OAC�����=
��3��3=
��
�ڡ�EF���ı���OEAF�����Ϊ1��2�����֣�
���OEF�������
��
=
��
��
=3��
��OA=OC����AOC=90�㣬
���OEF�ǵ���ֱ�������Σ�
��OE=OF��
��
OE•OF=
OE2=
��3��
��OE2=3��OE2=6��
����ֱ��AC�Ľ���ʽΪy=-x+3��
�����E��������a��-a+3����
��OE2=a2+��-a+3��2=2a2-6a+9��
��i��OE2=3ʱ��2a2-6a+9=3��
�����ã�a2-3a+3=0��
��=��-3��2-4��1��3=-3��0��
��ʱ�����⣻
��ii��OE2=6ʱ��2a2-6a+9=6��
�����ã�2a2-6a+3=0��
���a=
=
��
-a+3=-
+3=
��
��-a+3=-
+3=
��
���E��
��
����
��
����
��
|
���
|
�������ߵĹ�ϵʽΪy=
| 1 |
| 2 |
| 5 |
| 2 |
��2������D��DF��AC��F��
��y=0����
| 1 |
| 2 |
| 5 |
| 2 |
�����ã�x2-5x+6=0��
���x1=2��x2=3��
���D������2��0����AD=1��
��x=0����y=3��
���C������0��3����
��OC=OA=3��
���OAC�ǵ���ֱ�������Σ�
��AC=
| OA2+OC2 |
| 32+32 |
| 2 |
AF=DF=
| ||
| 2 |
| ||
| 2 |
��CF=AC-AF=3
| 2 |
| ||
| 2 |
5
| ||
| 2 |
��
| DF |
| CF |
| ||||
|
| 1 |
| 5 |
�ߡ�ACD+��ACP=45�㣬
����G��15��0����

��
| OC |
| OG |
| 3 |
| 15 |
| 1 |
| 5 |
CG�������ߵĽ���Ϊ��P��
��ֱ��CG�Ľ���ʽΪy=kx+b��
��
|
���
|
��y=-
| 1 |
| 5 |
����
|
���
|
|
���P������
| 23 |
| 5 |
| 52 |
| 25 |
��3���١�A��3��0����B��4��1����
��ֱ��AB��x��ļн�Ϊ45�㣬
���OAF=45�㣬
���OAF=��OCE=45�㣬
���ı���OEAF��Բ�ڽ��ı��Σ�
���OEC=��OFA��
�ڡ�OCE�͡�OAF�У�
|
���OCE�ա�OAF��AAS����
��S��OCE=S��OAF��

���ı���OEAF�����=��OAC�����=
| 1 |
| 2 |
| 9 |
| 2 |
�ڡ�EF���ı���OEAF�����Ϊ1��2�����֣�
���OEF�������
| 9 |
| 2 |
| 1 |
| 1+2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 2 |
| 1+2 |
��OA=OC����AOC=90�㣬
���OEF�ǵ���ֱ�������Σ�
��OE=OF��
��
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��OE2=3��OE2=6��
����ֱ��AC�Ľ���ʽΪy=-x+3��
�����E��������a��-a+3����
��OE2=a2+��-a+3��2=2a2-6a+9��
��i��OE2=3ʱ��2a2-6a+9=3��
�����ã�a2-3a+3=0��
��=��-3��2-4��1��3=-3��0��
��ʱ�����⣻
��ii��OE2=6ʱ��2a2-6a+9=6��
�����ã�2a2-6a+3=0��
���a=
6��
| ||
| 2��2 |
3��
| ||
| 2 |
-a+3=-
3+
| ||
| 2 |
3-
| ||
| 2 |
��-a+3=-
3-
| ||
| 2 |
3+
| ||
| 2 |
���E��
3+
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
3+
| ||
| 2 |
�����������Ƕ��κ����ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ������ϵ������һ�κ�������ʽ�����������ε�Ӧ�ã�����ֱ�������ε��ж������ʣ�ȫ�������ε��ж������ʣ�Բ�ڽ��ı��ε����ʣ��ۺ��Խ�ǿ���ѶȽϴ��������ո������ǽ���Ĺؼ���

��ϰ��ϵ�д�
 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д�
�����Ŀ
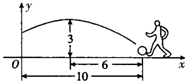 ��2013•��ɽ��ģ����һ����������У�һ��Ա��������ǰ��10�״�������ţ�������е�ˮƽ����Ϊ6��ʱ�ﵽ��ߵ㣬��ʱ���Ϊ3�ף�
��2013•��ɽ��ģ����һ����������У�һ��Ա��������ǰ��10�״�������ţ�������е�ˮƽ����Ϊ6��ʱ�ﵽ��ߵ㣬��ʱ���Ϊ3�ף�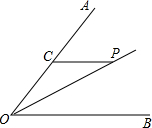 ��2013•��ɽ��ģ����ͼ����AOP=��BOP��CP��OB��CP=4����OC=��������
��2013•��ɽ��ģ����ͼ����AOP=��BOP��CP��OB��CP=4����OC=��������