题目内容
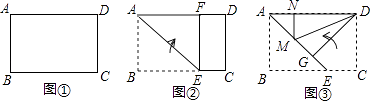
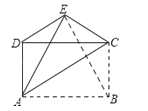
【题目】如图,已知矩形ABCD,把矩形沿直线AC折叠,点B落在点E处,连接DE、BE,若△ABE是等边三角形,则![]() =
= 
【答案】![]()
【解析】解: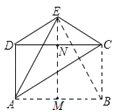
过E作EM⊥AB于M,交DC于N,
∵四边形ABCD是矩形,
∴DC=AB,DC∥AB,∠ABC=90°,
∴MN=BC,EN⊥DC,
∵延AC折叠B和E重合,△AEB是等边三角形,
∴∠EAC=∠BAC=30°,
设AB=AE=BE=2a,则BC=![]() a,
a,
即MN=![]() a,
a,
∵△ABE是等边三角形,EM⊥AB,
∴AM=a,由勾股定理得:EM=![]() =
=![]() a,
a,
∴△DCE的面积是![]() ×DC×EN=
×DC×EN=![]() ×2a×(
×2a×(![]() a﹣
a﹣![]() a)=
a)=![]() a2 ,
a2 ,
△ABE的面积是![]() AB×EM=
AB×EM=![]() ×2a×
×2a×![]() a=
a=![]() a2 ,
a2 ,
∴![]() =
=![]() =
=![]() ,
,
故答案为:![]() .
.
过E作EM⊥AB于M,交DC于N,根据矩形的性质得出DC=AB,DC∥AB,∠ABC=90°,设AB=AE=BE=2a,则BC=![]() a,即MN=
a,即MN=![]() a,求出EN,根据三角形面积公式求出两个三角形的面积,即可得出答案.
a,求出EN,根据三角形面积公式求出两个三角形的面积,即可得出答案.

练习册系列答案
相关题目