题目内容
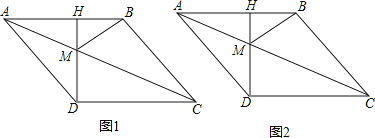
【题目】如图1,在平面直角坐标系中,将ABCD放置在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示,那么AD的长为 .

【答案】![]() .
.
【解析】
试题解析:①先经过点D,即AB>3,如图1:

设直线过点A时交x轴于点E,过点D交AB于点G,交x轴于点F,作DH⊥AB,
由图可知:OE=4,OF=7,DG=2![]() ,
,
∴EF=AG=OF-OE=3
∵直线y=-x
∴∠AGD=∠EFD=45°
∴△HGD是等腰直角三角形
∴DH=GH=![]() DG=
DG=![]() ×2
×2![]() =2
=2
∴AH=AG-GH=3-2=1
∴AD=![]()
②先经过点B,即AB=3,如图2:

设直线过点A时交x轴于点I,过点B时交AD于点K、x轴于点J,过点D时,交AB延长线于点N、x轴于点M,并过K点作KL⊥AB,
由图可知:OI=4,OJ=7,KB=2![]() ,OM=8,
,OM=8,
∴IJ=AB=3,IM=AN=4,
由直线y=-x,易得△KLB是等腰直角三角形,
∴KL=BL=![]() KB=
KB=![]() ×2
×2![]() =2,
=2,
∴AL=1,
∴AK=![]() ,
,
∵△ABK∽△AND,
∴![]() ,
,
即![]() ,
,
即AD=![]() .
.

练习册系列答案
相关题目