Question

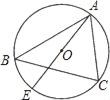
【题目】如图，△ABC是⊙O内接正三角形，将△ABC绕点O顺时针旋转30°得到△DEF，DE分别交AB，AC于点M，N，DF交AC于点Q，则有以下结论：①∠DQN=30°；②△DNQ≌△ANM；③△DNQ的周长等于AC的长；④NQ=QC．其中正确的结论是　 　．（把所有正确的结论的序号都填上）

Answer 1

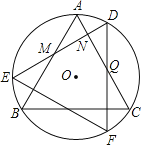
【答案】①②③

【解析】

试题如图，连接OA、OD、OF、OC、DC、AD、CF，

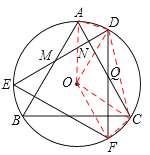
∵△ABC绕点O顺时针旋转30°得到△DEF，

∴∠AOD=∠COF=30°。

∴∠ACD=∠AOD=15°，∠FDC=∠COF=15°。

∴∠DQN=∠QCD+∠QDC=15°+15°=30°。所以①正确。

同理可得∠AMN=30°。

∵△DEF为等边三角形，∴DE=DF。∴弧DE=弧DF。∴弧AE+弧AD=弧DC+弧CF。

∵弧AD=弧CF，∴弧AE=弧DC。∴∠ADE=∠DAC。∴ND=NA。

在△DNQ和△ANM中，∵∠DQN=∠AMN，∠DNQ=∠ANM，DN=AN。

∴△DNQ≌△ANM（AAS）。所以②正确。

∵∠ACD=15°，∠FDC=15°，∴QD=QC。

∵ND=NA，∴ND+QD+NQ=NA+QC+NQ=AC，即△DNQ的周长等于AC的长。所以③正确。

∵△DEF为等边三角形，∴∠NDQ=60°。

∵∠DQN=30°，∴∠DNQ=90°。∴QD＞NQ。

∵QD=QC，∴QC＞NQ。所以④错误。

综上所述，正确的结论是①②③。