题目内容
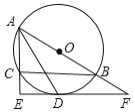
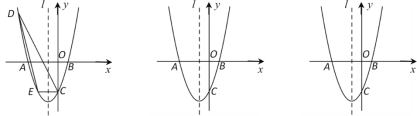
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .对称轴为直线
.对称轴为直线![]() ,点
,点![]() 在抛物线上.
在抛物线上.
(1)求直线![]() 的解析式;
的解析式;
(2)![]() 为直线
为直线![]() 下方抛物线上的一点,连接
下方抛物线上的一点,连接![]() 、
、![]() .当
.当![]() 的面积最大时,在直线
的面积最大时,在直线![]() 上取一点
上取一点![]() ,过
,过![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,连接
,连接![]() 、
、![]() .若
.若![]() 时,求
时,求![]() 的值;
的值;
(3)将抛物线![]() 沿
沿![]() 轴正方向平移得到新抛物线
轴正方向平移得到新抛物线![]() ,
,![]() 经过原点
经过原点![]() .
.![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() .设
.设![]() 是抛物线
是抛物线![]() 上任意一点,点
上任意一点,点![]() 在直线
在直线![]() 上,
上,![]() 能否成为以点
能否成为以点![]() 为直角顶点的等腰直角三角形?若能,直接写出点
为直角顶点的等腰直角三角形?若能,直接写出点![]() 的坐标.若不能,请说明理由.
的坐标.若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)能.
;(3)能.![]() ,
,![]() ,
,![]() ,
,![]()
【解析】
(1)求出C、D两点坐标,利用待定系数法即可解决问题;
(2)求出抛物线![]() 与
与![]() 轴交点
轴交点![]() 、
、![]() 两点的坐标,设
两点的坐标,设![]() ,则
,则![]() ,根据二次函数的性质求出E的坐标,可得当
,根据二次函数的性质求出E的坐标,可得当![]() 时,
时,![]() 最大,因为
最大,因为![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,过
,过![]() 作
作![]() 轴的垂线,由勾股定理得
轴的垂线,由勾股定理得![]() ,即可解决问题;
,即可解决问题;
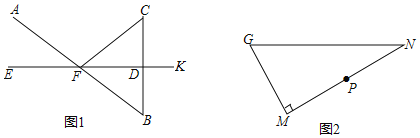
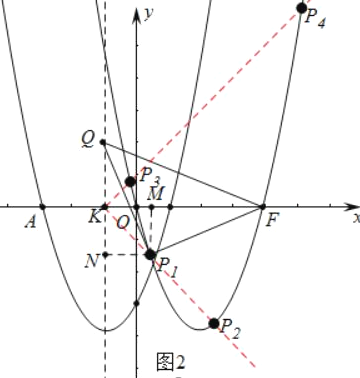
(3)存在.如图2中.作P1M⊥x轴于M,P1N⊥对称轴l于N.对称轴l交OA于K,由△P1MF≌△P1NQ,推出P1M=P1N,推出点P在∠MKN的角平分线上,只要求出直线KP1的解析式,构建方程组即可解决问题,同法可求P3,P4.
解:(1)∵当![]() 时,
时,![]() ,
,
∴![]() .
.
又∵![]() 在抛物线
在抛物线![]() 上,
上,
∴![]()
![]() ,
,
∴![]() .
.
设![]() 的解析式为
的解析式为![]() .
.
∴![]()
解得:![]()
∴![]() 的解析式为
的解析式为![]() .
.
(2) ∵令![]() ,
,
∴![]() .
.
解得:![]() .
.
∴![]() ,
, ![]() .
.
设![]() ,
,
∴![]() .
.
∴当![]() 时,
时,![]() 最大.
最大.
∴![]() .
.
又∵关于直线
![]() 的对称点为
的对称点为![]() ,
,
∴![]() 的垂直平分线交直线
的垂直平分线交直线![]() 于点
于点![]() ,
,
∴过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .
.
此时,![]() ,
,![]() ,
,![]() .
.
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() .
.
又∵直线![]() 与
与![]() 轴间的距离为1,
轴间的距离为1,
∴![]() .
.
(3)能.![]() ,
,![]() ,
,
![]() ,
,![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目