题目内容
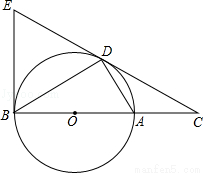
(2013年四川泸州2分)如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,点D的对称点F恰好落在BC上,已知折痕AE=10 cm,且tan∠EFC=
cm,且tan∠EFC= ,那么该矩形的周长为【 】
,那么该矩形的周长为【 】

A.72cm B.36cm C.20cm D.16cm
【答案】
A。
【解析】在矩形ABCD中,AB=CD,AD=BC,∠B=∠D=90°,
∵△ADE沿AE对折,点D的对称点F恰好落在BC上,∴∠AFE=∠D=90°,AD=AF。
∵∠EFC+∠AFB=180°﹣90°=90°,∠BAF+∠AFB=90°,∴∠BAF=∠EFC。
∵tan∠EFC= ,∴tan∠BAF =
,∴tan∠BAF = 。∴设BF=3x、AB=4x。
。∴设BF=3x、AB=4x。
在Rt△ABF中,根据勾股定理可得AF=5x,∴AD=BC=5x。∴CF=BC﹣BF=5x﹣3x=2x。
∵tan∠EFC= ,∴CE=CF•tan∠EFC=2x•
,∴CE=CF•tan∠EFC=2x• =
= x。∴DE=CD﹣CE=4x﹣
x。∴DE=CD﹣CE=4x﹣ x=
x= x。
x。
在Rt△ADE中,AD2+DE2=AE2,即(5x)2+( x)2=(10
x)2=(10 )2,整理得,x2=16,解得x=4。
)2,整理得,x2=16,解得x=4。
∴AB=4×4=16cm,AD=5×4=20cm,矩形的周长=2(16+20)=72cm。故选A。
考点:翻折变换(折叠问题),矩形的性质,勾股定理,锐角三角函数定义。

练习册系列答案
相关题目
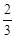 ,求BE的长.
,求BE的长.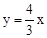 与反比例函数
与反比例函数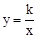 (x>0)的图象交于点A.将
(x>0)的图象交于点A.将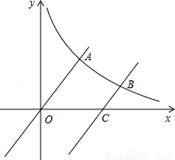
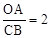 ,求反比例函数的解析式.
,求反比例函数的解析式.