题目内容
若关于x的方程ax2-2（a-3）x+（a-13）=0至少有一个整数根，求非负整数a的值．分析：因为根的表示式复杂，从韦达定理得出的a的两个关系式中消去a也较困难，又因a的次数低于x的次数，故可将原方程变形为关于a的一次方程．
解答：解：a=
=
≥1①
解得：-6≤x≤2且x≠1，
∴x=-6，-5，-4，-3，-2，-1，0，2
分别代入①式得：a=1，
，
，
，
，
，13，1．
∵因为分数不合题意舍去，故a=1，13．
非负整数a的值是1，13．
| 13-6x |
| x2-2x+1 |
| 13-6x |
| (x-1)2 |
解得：-6≤x≤2且x≠1，
∴x=-6，-5，-4，-3，-2，-1，0，2
分别代入①式得：a=1，
| 43 |
| 36 |
| 37 |
| 25 |
| 31 |
| 16 |
| 25 |
| 9 |
| 19 |
| 4 |
∵因为分数不合题意舍去，故a=1，13．
非负整数a的值是1，13．
点评：此题主要考查了一元二次方程整数解的有关知识，关键是确定a与x之间的函数关系．
练习册系列答案
相关题目
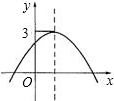如图，是二次函数y=ax2+bx+c的图象，若关于x的方程ax2+bx+c-k=0有两个不相等的实数根，则k的取值范围是（ ）| A、k＜3 | B、k＞3 | C、k≤3 | D、k≥3 |