题目内容
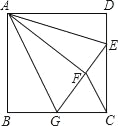
【题目】如图，在长方形
中，
，
，动点
、
分别从点
、
同时出发，点以2厘米/秒的速度向终点
移动，点以1厘米/秒的速度向
移动，当有一点到达终点时，另一点也停止运动.设运动的时间为
，问：
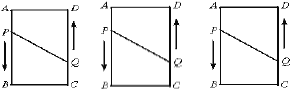
(1)当
秒时，四边形
面积是多少？
(2)当为何值时，点和点距离是
？
(3)当
_________时，以点、、为顶点的三角形是等腰三角形.(直接写出答案)
【答案】（1）5厘米2；（2）
秒或
秒；（3）
秒或
秒或
秒或
秒.
【解析】
试题（1）求出BP，CQ的长，即可求得四边形BCQP面积.
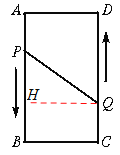
（2）过Q点作QH⊥AB于点H，应用勾股定理列方程求解即可.
（3）分PD=DQ，PD=PQ，DQ=PQ三种情况讨论即可.
（1）当t=1秒时，BP=6-2t=4，CQ=t=1，
∴四边形BCQP面积是
厘米2.
（2）如图，过Q点作QH⊥AB于点H，则PH=BP-CQ=6-3t，HQ=2，
根据勾股定理，得
， 解得
.
∴当
秒或
秒时，点P和点Q距离是3cm.
（3）∵
，
当PD=DQ时，
，解得
或
（舍去）；
当PD=PQ时，
，解得
或
（舍去）；
当DQ=PQ时，
，解得
或
.
综上所述，当秒或秒或秒或秒时， 以点P、Q、D为顶点的三角形是等腰三角形.
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
