Question

如果依次连接四边形各边的中点所得四边形是矩形，那么原来的四边形的两条对角线（ ）
A．相等
B．互相垂直
C．互相平分
D．互相平分且相等

Answer 1

【答案】分析：由于顺次连接四边形各边中点得到的四边形是平行四边形，再由矩形的判定可知，依次连接对角线互相垂直的四边形各边的中点所得四边形是矩形．
解答：解：由矩形的性质知，矩形的四个角为直角，即每组邻边互相垂直，故原四边形的对角线应互相垂直．
顺次连接对角线互相垂直的四边形的各边中点所得的图形是矩形．
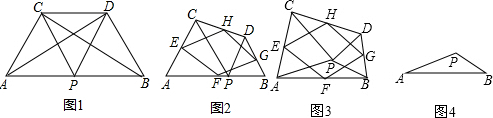
如图：∵E、F、G、H分别为各边中点，
∴EF∥GH∥DB，EF=GH=DB，
EH=FG=AC，EH∥FG∥AC，
∵DB⊥AC，
∴EF⊥EH
∴四边形EFGH是矩形．
故选B．
点评：此题主要考查了矩形的判定定理，画出图形进而应用平行四边形的判定以及矩形判定是解决问题的关键．