题目内容
(A)方程 的解为________
的解为________
(B)方程 的解是________.
的解是________.
x=-1 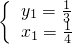 或者
或者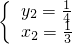
分析:(A)方程的两边同时乘以最简公分母2x(x-1),把分式方程化简为整式方程,求x的值即可,最后把x的值代入最简公分母进行检验,若x的值使最简公分母为零,则原方程无实数解;(B)通过方程①,推出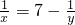 ③,然后把③代入方程②,解分式方程,即可求出y的值,然后把y的值代入到③,即可推出x的值.
③,然后把③代入方程②,解分式方程,即可求出y的值,然后把y的值代入到③,即可推出x的值.
解答:(A)∵ ,
,
∴方程的两边同时乘以2x(x-1)得:4x2+(x-1)2=2×2x(x-1),
整理得:x2+2x+1=0,
∴(x+1)2=0,
∴x=-1,
检验:当x=-1时,2x(x-1)=-2×(-2)=4≠0,
所以,x=-1是原方程的解.
(2)∵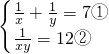 ,
,
∴由①得: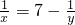 ③,
③,
∴把③代入②得: (7-
(7- )=12,
)=12,
整理得: -
- =12,
=12,
方程两边同乘以y2得:12y2-7y+1=0,
∴(3y-1)(4y-1)=0,
∴y1= ,y2=
,y2= ,
,
检验:当y1= 时,y2=
时,y2= ≠0,所以y1=
≠0,所以y1= 为方程的解,
为方程的解,
当y2= 时,y2=
时,y2= ≠0,所以y2=
≠0,所以y2= 为方程的解,
为方程的解,
∴把y1= 代入③得:x=
代入③得:x= ;
;
把y2= 代入③得:x=
代入③得:x= ,
,
∴原方程的解为: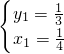 或者
或者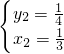 ,
,
故答案为x=-1;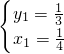 或者
或者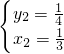 .
.
点评:本题主要考查解分式方程,解分式方程组,解题的关键在于(1)通过方程两边同乘以最简公分母,对分式方程进行化简,(2)通过对第一个方程的变形,用含x的表达式表示 ,熟练运用代入法求出y.
,熟练运用代入法求出y.
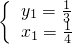 或者
或者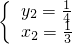
分析:(A)方程的两边同时乘以最简公分母2x(x-1),把分式方程化简为整式方程,求x的值即可,最后把x的值代入最简公分母进行检验,若x的值使最简公分母为零,则原方程无实数解;(B)通过方程①,推出
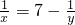 ③,然后把③代入方程②,解分式方程,即可求出y的值,然后把y的值代入到③,即可推出x的值.
③,然后把③代入方程②,解分式方程,即可求出y的值,然后把y的值代入到③,即可推出x的值.解答:(A)∵
 ,
,∴方程的两边同时乘以2x(x-1)得:4x2+(x-1)2=2×2x(x-1),
整理得:x2+2x+1=0,
∴(x+1)2=0,
∴x=-1,
检验:当x=-1时,2x(x-1)=-2×(-2)=4≠0,
所以,x=-1是原方程的解.
(2)∵
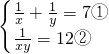 ,
,∴由①得:
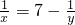 ③,
③,∴把③代入②得:
 (7-
(7- )=12,
)=12,整理得:
 -
- =12,
=12,方程两边同乘以y2得:12y2-7y+1=0,
∴(3y-1)(4y-1)=0,
∴y1=
 ,y2=
,y2= ,
,检验:当y1=
 时,y2=
时,y2= ≠0,所以y1=
≠0,所以y1= 为方程的解,
为方程的解,当y2=
 时,y2=
时,y2= ≠0,所以y2=
≠0,所以y2= 为方程的解,
为方程的解,∴把y1=
 代入③得:x=
代入③得:x= ;
;把y2=
 代入③得:x=
代入③得:x= ,
,∴原方程的解为:
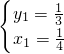 或者
或者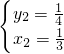 ,
,故答案为x=-1;
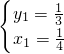 或者
或者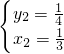 .
.点评:本题主要考查解分式方程,解分式方程组,解题的关键在于(1)通过方程两边同乘以最简公分母,对分式方程进行化简,(2)通过对第一个方程的变形,用含x的表达式表示
 ,熟练运用代入法求出y.
,熟练运用代入法求出y. 
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目