题目内容
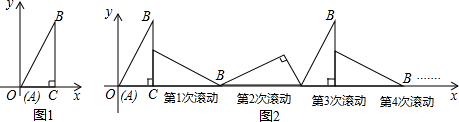
（2013•长清区二模）如图1，Rt△ABC中，∠ACB=90°，AC=1，BC=2，将△ABC放置在平面直角坐标系中，使点A与原点重合，点C在x轴正半轴上．将△ABC按如图2方式顺时针滚动（无滑动），则滚动2013次后，点B的坐标为
（2014+671
，2）
| 5 |
（2014+671
，2）
．| 5 |
分析：根据三角形的滚动规律分别得出B点的横、纵坐标，进而得出答案．
解答：解：根据三角形滚动规律得出每3次一循环，
∵2013÷3=671，
∴滚动2013次后，点B的纵坐标与滚动第3次纵坐标相同为2，
∵∠ACB=90°，AC=1，BC=2，
∴OB=
=
，
∴三角形三边长的和为：1+2+
=3+
，
则滚动2013次后，点B的横坐标为：1+671（3+
）=2014+671
．
故点B的坐标为：（2014+671
，2）．
故答案为：（2014+671
，2）．
∵2013÷3=671，
∴滚动2013次后，点B的纵坐标与滚动第3次纵坐标相同为2，
∵∠ACB=90°，AC=1，BC=2，
∴OB=
| 12+22 |
| 5 |
∴三角形三边长的和为：1+2+
| 5 |
| 5 |
则滚动2013次后，点B的横坐标为：1+671（3+
| 5 |
| 5 |
故点B的坐标为：（2014+671
| 5 |
故答案为：（2014+671
| 5 |
点评：此题主要考查了点的坐标规律，根据已知得出点的变化规律是解题关键．
练习册系列答案
阶梯计算系列答案
相关题目
（2013•长清区二模）如图，甲、乙两图是分别由五个棱长为“1”的立方块组成的两个几何体，它们的三视图中完全一致的是（ ）
（2013•长清区二模）如图，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在线段BC上，且AE=CF．
（2013•长清区二模）如图，一个正在绘制的扇形统计图，整个圆表示某班参加体育活动的总人数，那么表示参加实心球训练的人数占总人数的35%的扇形是（ ）