题目内容
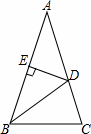
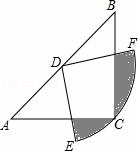
如图,在△ABC中,CA=CB,∠ACB=90°,以AB的中点D为圆心,作圆心角为90°的扇形DEF,点C恰在EF上,设∠BDF=α(0°<α<90°),当α由小到大变化时,图中阴影部分的面积( )
|
| A. | 由小到大 | B. | 由大到小 |
|
| C. | 不变 | D. | 先由小到大,后由大到小 |
C解:作DM⊥AC于M,DN⊥BC于N,连接DC,
∵CA=CB,∠ACB=90°,
∴∠A=∠B=45°,
DM= AD=
AD= AB,DN=
AB,DN= BD=
BD= AB,
AB,
∴DM=DN,
∴四边形DNCN是正方形,
∴∠MDN=90°,
∴∠MDG=90°﹣∠GDN,
∵∠EDF=90°,
∴∠NDH=90°﹣∠GDN,
∴∠MDG=∠NDH,
在△DMG和△DNH中,
 ,
,
∴△DMG≌△DNH,
∴四边形DGCH的面积=正方形DMCN的面积,
∵正方形DMCN的面积=DM2= AB2,
AB2,
∴四边形DGCH的面积= ,
,
∵扇形FDE的面积= =
= ,
,
∴阴影部分的面积=扇形面积﹣四边形DGCH的面积= (定值),
(定值),


练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
某化妆品专卖店,为了吸引顾客,在“母亲节”当天举办了甲、乙两种品牌化妆品有奖酬宾活动,凡购物满88元,均可得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机中一次连续摇出两个球,根据球的颜色决定送礼金券的多少(如下表):
| 甲种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 6 | 12 | 6 |
| 乙种品牌 化妆品 | 球 | 两红 | 一红一白 | 两白 |
| 礼金卷(元) | 12 | 6 | 12 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率;
(2)如果一个顾客当天在本店购物满88元,若只考虑获得最多的礼品卷,请你帮助分析选择购买哪种品牌的化妆品?并说明理由.
方程2x﹣1=3的解是( )
|
| A. | ﹣1 | B. | ﹣2 | C. | 1 | D. | 2 |

 ,则x2﹣y2的值为
,则x2﹣y2的值为