��Ŀ����
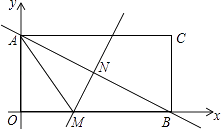
����Ŀ����ͼ1����ֱ������ϵ�У���֪��A��0��2������B��-2��0��������B���߶�OA���е�C��ֱ��BC�����߶�BCΪ��������������BCDE.
��1����գ���D������Ϊ_________����E������Ϊ_______________.
��2����������![]() ����A��D��E���㣬��������ߵĽ���ʽ.
����A��D��E���㣬��������ߵĽ���ʽ.
��3���������κ������߾���ÿ��![]() ����λ���ȵ��ٶ�������BCͬʱ����ƽ�ƣ�ֱ�������εĶ���E����
����λ���ȵ��ٶ�������BCͬʱ����ƽ�ƣ�ֱ�������εĶ���E����![]() ����ʱ�������κ������߾�ֹͣ�˶�.
����ʱ�������κ������߾�ֹͣ�˶�.
�����˶������У�������������y���Ҳಿ�ֵ����Ϊ![]() ����
����![]() ����ƽ��ʱ��
����ƽ��ʱ��![]() ���룩�ĺ�����ϵʽ����д����Ӧ�Ա���
���룩�ĺ�����ϵʽ����д����Ӧ�Ա���![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���˶�ֹͣʱ���������ߵĶ�������.
���𰸡���1��D������Ϊ��-1��3����E������Ϊ��-3��2����
��2�������ߵĽ���ʽΪ![]() ��
��
��3����S��x�ĺ�����ϵʽΪ��
��0��t��![]() ʱ, S=5
ʱ, S=5![]()
��![]() ��t��1ʱ��S=5t
��t��1ʱ��S=5t![]()
��1��t��![]() ʱ��S=-5t2+15t
ʱ��S=-5t2+15t![]()
�������ߵĶ��������ǣ�![]() ��
�� ![]() ��.
��.
����������1��D��-1��3����E��-3��2����2�֣�
��2�������߾�����0��2������-1��3������-3��2������
![]()
��� ![]()
��![]()
��3���ٵ���D�˶���y����ʱ��t=![]() .
.
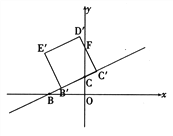
��0��t��![]() ʱ������ͼ
ʱ������ͼ
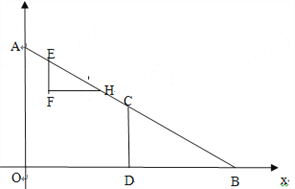
��D��C����y���ڵ�F
��tan��BCO= ![]() =2,�֡ߡ�BCO=��FCC��
=2,�֡ߡ�BCO=��FCC��
��tan��FCC��=2, ��![]() =2
=2
��CC��= ![]() t,��FC��=2
t,��FC��=2![]() t.
t.
��S��CC��F =![]() CC�䡤FC��=
CC�䡤FC��= ![]() t��
t��![]() t=5 t2
t=5 t2
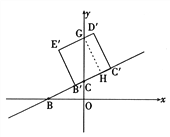 ����B�˶�����Cʱ��t=1.��
����B�˶�����Cʱ��t=1.��![]() ��t��1ʱ������ͼ
��t��1ʱ������ͼ
��D��E����y���ڵ�G����G��GH��B��C����H.
��Rt��BOC��BC= ![]()
��GH= ![]() ,��CH=
,��CH=![]() GH=
GH= ![]()
��CC��=![]() t,��HC��=
t,��HC��=![]() t-
t-![]() ,��GD��=
,��GD��=![]() t-
t-![]()
��S����CC��D��G =![]() (
(![]() t-
t-![]() +
+ ![]() t)
t) ![]() =5t-
=5t-![]()
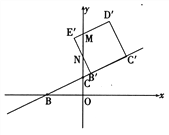 ����E�˶���y����ʱ��t=
����E�˶���y����ʱ��t=![]() .
.
��1��t��![]() ʱ������ͼ��ʾ
ʱ������ͼ��ʾ
��D��E����E��B���ֱ�y���ڵ�M��N
��CC��=![]() t��B��C��=
t��B��C��=![]() ,
,
��CB��=![]() t-
t-![]() ,��B��N=2CB��=
,��B��N=2CB��=![]() t-
t-![]()
��B��E��=![]() ,��E��N=B��E��-B��N=
,��E��N=B��E��-B��N=![]() -
-![]() t
t
��E��M=![]() E��N=
E��N=![]() (
(![]() -
-![]() t)
t)
��S��MNE�� =![]() (
(![]() -
-![]() t)��
t)��![]() (
(![]() -
-![]() t)=5t2-15t+
t)=5t2-15t+![]()
��S�����B��C��D��MN =S������B��C��D��E�� -S��MNE�� =![]() (5t2-15t+
(5t2-15t+![]() )=-5t2+15t-
)=-5t2+15t-![]()
����������S��x�ĺ�����ϵʽΪ��
��0��t��![]() ʱ, S=5
ʱ, S=5![]()
��![]() ��t��1ʱ��S=5t
��t��1ʱ��S=5t![]()
��1��t��![]() ʱ��S=-5t2+15t
ʱ��S=-5t2+15t![]()
�ڵ���E�˶�����E��ʱ���˶�ֹͣ.����ͼ��ʾ
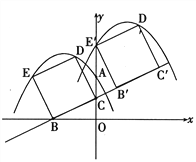 �ߡ�CB��E��=��BOC=90������BCO=��B��CE��
�ߡ�CB��E��=��BOC=90������BCO=��B��CE��
���BOC�ס�E��B��C
��![]()
��OB=2��B��E��=BC=![]()
��![]()
��CE��=![]()
��OE��=OC+CE��=1+![]() =
=![]()
��E����0��![]() ��
��
�ɵ�E��-3��2���˶�����E����0�� ![]() ��,��֪��������������ƽ����3����λ������ƽ����
��,��֪��������������ƽ����3����λ������ƽ����![]() ����λ.
����λ.
��![]() =
= ![]()
��ԭ�����߶�������Ϊ��![]() ��
�� ![]() ��
��
���˶�ֹͣʱ�������ߵĶ�������Ϊ��![]() ��
�� ![]() ��
��

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д� ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�