Question

【题目】如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax2﹣10ax+c经过点C，顶点M在直线BC上．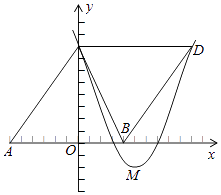

（1）证明四边形ABCD是菱形，并求点D的坐标；
（2）求抛物线的对称轴和函数表达式；
（3）在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）证明：∵A（﹣6，0），B（4，0），C（0，8），

∴AB=6+4=10，AC= =10，

∴AB=AC，

由翻折可得，AB=BD，AC=CD，

∴AB=BD=CD=AC，

∴四边形ABCD是菱形，

∴CD∥AB，

∵C（0，8），

∴点D的坐标是（10，8）

（2）解：∵y=ax2﹣10ax+c，

∴对称轴为直线x=﹣ =5．

设M的坐标为（5，n），直线BC的解析式为y=kx+b，

∴ ，

解得 ．

∴y=﹣2x+8．

∵点M在直线y=﹣2x+8上，

∴n=﹣2×5+8=﹣2．

又∵抛物线y=ax2﹣10ax+c经过点C和M，

∴ ，

解得 ．

∴抛物线的函数表达式为y= x2﹣4x+8

（3）解：存在．

理由如下：由题意可知，P在抛物线y= x2﹣4x+8上，且到BD，CD所在直线距离相等，所以P在二次函数与BD、CD所在的直线的夹角平分线的交点上，而BD、CD所在的直线的夹角平分线有两条：一条是AD所在的直线，解析式为y= x+3，另外一条是过D且与BC平行的直线，解析式为y=﹣2x+28，

联立 ，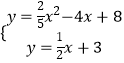

解得： （舍）或 ，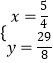

联立 ，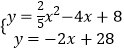

解得： （舍）或

所以当△PBD与△PCD的面积相等，点P的坐标为P1（ ， ），P2（﹣5，38）

【解析】（1）根据两点之间的距离公式，勾股定理，翻折的性质得AB=BD=CD=AC，根据菱形的性质和判定得出D点的坐标；（2)根据对称轴公式得出抛物线的对称轴，设M的坐标为（5，n），直线BC的解析式为y=kx+b，根据待定系数法可得出M点的坐标，再根据待定系数法求出抛物线的解析式；（3)分点P在CD的上面和点P在CD的下面两种情况，根据等底等高的三角形面积相等即可求出P点的坐标。
【考点精析】认真审题，首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．