题目内容
在同一直角坐标系中，函数y=mx+m和y=﹣mx2+2x+2（m是常数，且m≠0）的图象可能是
A． | B． | C． | D． |
D
解析试题分析：根据一次函数和二次函数的图象与系数的关系，分两种情况讨论：
当m＞0时，函数y=mx+m的图象经过一、二、三象限，函数y=﹣mx2+2x+2的图象开口向下，所给选项中没有满足条件的选项；
当m＜0时，函数y=mx+m的图象经过二、三、四象限，函数y=﹣mx2+2x+2的图象开口向上，且对称轴
＜0。即二次函数图象的对称轴在y轴左侧，所给选项中满足条件的是选项D。
故选D。
练习册系列答案
相关题目
二次函数y=ax2+bx+c图象上部分点的坐标满足下表：
| x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| y | … | ﹣3 | ﹣2 | ﹣3 | ﹣6 | ﹣11 | … |
A．(﹣3，﹣3) B． (﹣2，﹣2) C． (﹣1，﹣3) D． (0，﹣6)
二次函数
的图象如图所示，则m的值是
| A．－8 | B．8 | C．±8 | D．6 |
若二次函数
(a≠0)的图象与x轴有两个交点，坐标分别为(x1，0)，(x2，0)，且x1<x2，图象上有一点M (x0，y0)在x轴下方，则下列判断正确的是
| A．a>0 | B．b2－4ac≥0 |
| C．x1<x0<x2 | D．a(x0－x1)( x0－x2)<0 |
小轩从如图所示的二次函数y=ax2+bx+c（a≠0）的图象中，观察得出了下面五条信息：
①ab＞0；②a+b+c＜0；③b+2c＞0；④a﹣2b+4c＞0；⑤
．
你认为其中正确信息的个数有
| A．2个 | B．3个 | C．4个 | D．5个 |
如图，等边三角形ABC的边长为3，N为AC的三等分点，三角形边上的动点M从
点A出发，沿A→B→C的方向运动，到达点C时停止．设点M运动的路程为x，MN2=y，则y关于x的函数图象大致为
A． | B． | C． | D． |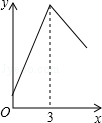
若一次函数y=ax+b（a≠0）的图象与x轴的交点坐标为（﹣2，0），则抛物线y=ax2+bx的对称轴为【 】
| A．直线x=1 | B．直线x=﹣2 | C．直线x=﹣1 | D．直线x=﹣4 |
的图象如图所示，则一次函数
与反比例函数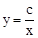
在同一平面直角坐标系中的大致图象为【 】
