题目内容
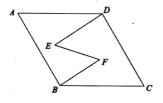
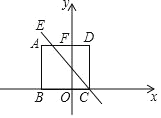
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]()
(1) 将![]() 向右平移6个单位长度至
向右平移6个单位长度至![]() , 再将
, 再将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 至
至![]() ,请按要求画出图形;
,请按要求画出图形;
(2)在![]() 的变换过程中,直接写出点
的变换过程中,直接写出点![]() 的运动路径长
的运动路径长
(3)![]() 可看成
可看成![]() 绕某点
绕某点![]() 旋转
旋转![]() 得到的, 则点
得到的, 则点![]() 的坐标为
的坐标为

【答案】(1)图见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用点平移的坐标规律得出点![]() 的坐标,然后描点、顺次连接即可得
的坐标,然后描点、顺次连接即可得![]() ;利用旋转的性质画出点
;利用旋转的性质画出点![]() ,再顺次连接即可得
,再顺次连接即可得![]() ;
;
(2)点C的运动路径长为平移的距离与弧![]() 的长之和,先求出
的长之和,先求出![]() 的长,再利用弧长公式计算即可得;
的长,再利用弧长公式计算即可得;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点即为点P,点绕某点(非原点)旋转
的垂直平分线,它们的交点即为点P,点绕某点(非原点)旋转![]() 的坐标变换规律得出点
的坐标变换规律得出点![]() 的坐标,再设点P的坐标为
的坐标,再设点P的坐标为![]() ,根据点绕某点(非原点)旋转
,根据点绕某点(非原点)旋转![]() 的坐标变换规律可得一个关于a、b的二元一次方程组,求解即可得.
的坐标变换规律可得一个关于a、b的二元一次方程组,求解即可得.
(1)由点平移的坐标规律得:![]()
即![]()
描点、顺次连接得到![]() ,如图所示:
,如图所示:
由旋转的性质画出点![]() ,再顺次连接得到
,再顺次连接得到![]() ,如图所示:
,如图所示:
(2)由平移的性质得:![]()
![]()
![]()
![]() 弧
弧![]() 的长为
的长为![]()
则点![]() 的运动路径长为
的运动路径长为![]()
故答案为:![]() ;
;
(3)作![]() 和
和![]() 的垂直平分线,它们的交点即为点P,如图所示:
的垂直平分线,它们的交点即为点P,如图所示:
理由:由旋转的性质可知,![]()
由线段垂直平分线的性质得:点P既在![]() 的垂直平分线上,也在
的垂直平分线上,也在![]() 的垂直平分线上
的垂直平分线上
则它们的交点即为点P
点P的坐标求解过程如下:
由点绕某点(非原点)旋转![]() 的坐标变换规律得:
的坐标变换规律得:![]()
即![]()
设点P的坐标为![]()
则有![]()
解得![]()
故点P的坐标为![]()
故答案为:![]() .
.


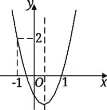
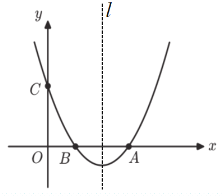
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 是常数,
是常数,![]() )的自变量x与函数值y的部分对应值如下表:
)的自变量x与函数值y的部分对应值如下表:
| … | -1 | 0 | 1 | 3 | … |
| … |
| 3 |
| 3 | … |
且当![]() 时,与其对应的函数值
时,与其对应的函数值![]() .有下列结论:①
.有下列结论:①![]() ;②3是关于
;②3是关于![]() 的方程
的方程![]() 的一个根;③
的一个根;③![]() .其中,正确结论的个数是( )
.其中,正确结论的个数是( )
A.0B.1C.2D.3
【题目】为了帮助我市一名贫困学生,某校组织捐款,现从全校所有学生的捐款数额中随机抽取10名学生的捐款数统计如下表:
捐款金额/元 | 20 | 30 | 50 | 90 |
人数 | 2 | 4 | 3 | 1 |
则下列说法正确的是( )
A. 10名学生是总体的一个样本
B. 中位数是40
C. 众数是90
D. 方差是400